BUAA-OO-2024-Unit3

前言——唉，JML

本单元的主题为基于规格的层次化设计，相较于前两个单元的问题抽象与分解、并发程序设计，这单元的难度算是降低了不少吧——所有的方法与接口都由 $\mathcal{JML}$ 规格给出，只需要根据约定、将功能一一实现即可（暂不考虑程序性能的前提下）。

在我看来，其实不用太纠结于 $\mathcal{JML}$ 这里有什么毛病，那里有什么毛病，~~虽然有时看起来确实很滑稽~~（比如由于其形式化的描述，费了老半天劲写出来的东西自然语言一句话就讲明白了），最主要的一点还是去感受契约式设计的魅力（~~见仁见智把~~）。

规格设计者（架构师）基于规格和需要实现的业务，定义一个类所需管理的数据及其需要满足的约束和实现不同作用的方法；而程序员则遵循对每个对象和方法的要求，只需聚焦于具体方法的实现。当然在保证没有二义性的前提下， $\mathcal{JML}$ 大篇大篇的数理逻辑表述确实又臭又长（所以这学期助教们对用于教学的JML的简化工作确实挺好的）。不过 $\mathcal{JML}$ 这样的形式化的表述，在另一方面确实有利于对代码进行各种验证和测试：

\tt pre\text{-}condition \to post\text{-}condition \, \, \And\And \, \, no \, side\text{-}effects

所以在实际项目开发过程中，感觉自然语言和规格语言并不应该是相斥的，不是只能有一个存在。~~（教学中只给JML并要求能看懂，倒也能理解）~~

还有一点要说的是， $\mathcal{JML}$ 描述的规格是我们希望我们管理的数据会产生什么样的行为/变化，在实际实现的过程中我们不应逐字逐句翻译 $\mathcal{JML}$ （一些时候无法满足性能要求甚至~~难以翻译~~），而应采用合适的算法、数据结构，以及将方法的逻辑拆解成小的功能模块；另外，如果我们要写出一个已实现的方法对应的 $\mathcal{JML}$ （虽然感觉这个行为很难评），也不能一句一句翻译，比如这个方法用了某种算法，那使用的算法的细节并不是 $\mathcal{JML}$ 或者说规格关心的，关注的是数据或者对象状态的变化。比如下面这个求解字符串莱文斯坦距离的例子：

public class Levenshtein {
    private static int[][] dp;
    /*@ requires str1 != null && str2 != null;
      @ ensures \result ==
      @     ((str1.length() == str2.length() && (\forall int i; 0 <= i && i < str1.length(); str1.charAt(i) == str2.charAt(i))) ||
      @      (str1.length() == str2.length() - 1 && (\forall int i; 0 <= i && i < str1.length(); str1.charAt(i) == str2.charAt(i))) ||
      @      (str1.length() - 1 == str2.length() && (\forall int i; 0 <= i && i < str2.length(); str1.charAt(i) == str2.charAt(i))));
      @*/
    public boolean check(String str1, String str2) {//使用某些方法帮助简化JML
        if (str1 == null || str2 == null) { return false; }
        if (str1.equals(str2)) { return true; }
        String tmp = str1.substring(0, str1.length() - 1);
        if (tmp.equals(str2)) { return true; }
        tmp = str2.substring(0, str2.length() - 1);
        return str1.equals(tmp);
    }
    
    /*@ public normal_behavior
      @ requires src != null && dst != null && !src.equals(dst);
      @ ensures (\exist String[] PathM;
                pathM.length >= 2 && pathM[0].equals(src) && pathM[pathM.length - 1].equals(dst) &&
                (\forall int i; 1 <= i && i < pathM.length; check(pathM[i - 1], pathM[i]));
                (\forall String[] Path; Path.length >= 2 && path[0].equals(src) && path[path.length - 1].equals(dst) &&
                 (\forall int i; 1 <= i && i < path.length; check(path[i - 1], path[i]));
                 (\sum int i; 0 <= i && i < path.length; 1) >= (\sum int i; 0 <= i && i < pathM.length; 1) &&
                 \result == (\sum int i; 1 <= i && i < pathM.length; 1)));
      @ also
      @ public normal_behavior
      @ requires src != null && dst != null && src.equals(dst);
      @ ensures \result == 0
      @*/
    public static int solve(String src, String dst) {
        dp = new int[src.length() + 1][dst.length() + 1];
        for (int i = 0; i < src.length(); ++i) {
            dp[i + 1][0] = i + 1;
        }
        for (int i = 0; i < dst.length(); ++i) {
            dp[0][i + 1] = i + 1;
        }
        for (int i = 0; i < src.length(); ++i) {
            for (int j = 0; j < dst.length(); ++j) {
                dp[i + 1][j + 1] = Math.min(dp[i][j + 1], dp[i + 1][j]) + 1;
                dp[i + 1][j + 1] = Math.min(dp[i][j] + 1, dp[i + 1][j + 1]);
                if (src.charAt(i) == dst.charAt(j)) {
                    dp[i + 1][j + 1] = Math.min(dp[i + 1][j + 1], dp[i][j]);
                }
            }
        }
        return dp[src.length()][dst.length()];
    }
}

关于测试

黑盒测试与白盒测试

黑盒测试：

基于代码的规格说明和功能需求进行的测试
作为测试人员，我们不需要了解代码的内部结构或实现细节，而是将其视为一个黑盒子，只关注其输入和输出之间的关系，检验对错（设置各种Corner Cases以及压力测试等）
这类测试主要是用于验证代码的行为是否符合预期
这单元我们根据 $\mathcal{JML}$ 规格进行的测试就属于黑盒测试

白盒测试：

基于代码的内部结构和实现细节进行的测试
我们需要了代码内部逻辑和使用的算法，并针对地设计测试用例
通常需要关注代码覆盖率、分支覆盖率等各种覆盖率，比如上学期 $\mathcal{OOP}$ 要求的 $\mathcal{JUnit}$

其他多种测试

单元测试
- 单元测试是针对软件中的最小可测试单元进行的测试，通常是代码中的一个函数、方法或类。
- 单元测试的目标是验证每个单元的功能是否符合预期，以确保代码的每个部分都能正常工作。
- 例如，本单元对社交网络的单元测试可以包括对各种增加/删除元素、查询、发送信息等功能进行测试，每个功能被视为一个单元。
功能测试
- 功能测试是测试软件的功能是否按照规格说明和用户需求的预期工作。
- 在功能测试中，我们需要模拟用户操作，验证软件的各项功能是否符合预期，包括输入验证、功能流程、界面交互等。
- 例如，对于一个电子商务网站，功能测试可以包括用户注册、浏览商品、下订单、支付等功能的测试。
集成测试
- 集成测试是测试软件中不同模块或组件之间的交互和集成是否正常。
- 在集成测试中，我们需要将各个模块组合起来，并测试它们之间的接口和交互是否符合设计要求。
- 例如，对于一个社交网络应用，集成测试可以包括用户登录、发布动态、评论、点赞等功能的整体测试。
压力测试
- 压力测试是测试软件在负载过高或资源不足的情况下是否能够正常工作。
- 在压力测试中，我们可以模拟大量用户同时访问系统或者增加系统负载，以测试软件的性能、稳定性和可靠性。
- 例如，对于一个在线游戏服务器，压力测试可以模拟大量玩家同时在线、进行游戏，以测试服务器是否能够承受住这样的负载。或者对于我们~~喜闻乐见~~的互测来说，生成各种极限数据。
回归测试
- 回归测试是在软件发生变更后重新执行之前的测试用例，以确保变更不会对软件的其他部分造成影响。
- 在回归测试中，我们需要针对变更的部分以及相关联的功能重新执行测试用例，并验证软件的整体功能是否受到影响。
- 例如，当我们每次修复bug或者进行迭代后，也要使用之前已经通过的数据对代码进行测试，以确保bug修复没有引入新的问题😃

总之，这些测试类型在软件或项目开发过程中起着不同的作用，我们可以通过综合运用有效地提高软件的质量、可靠性、可维护性。

数据构造策略

除了使用大佬们提供的评测机，我构造数据的主要策略是，针对一些需要优化的指令进行压力测试。

比如第二次互测时，对于指令queryTagValueSum，我构造数据的具体策略如下：

load_network（100人）
at 1 1（给 $person1$ 加上Tag）
增加 $n$ 个人并与 $person1$ 连边，然后连同前面的 $99$ 个人，一块加入上述Tag中
最后剩下的操作全部执行qtvs

简单计算可知， $n$ 取约 $725$ 时压力最大（针对双重循环来说）。

架构设计

本单元的主要任务是实现一个简单的社交网络。

具体的UML类图如下

hw11

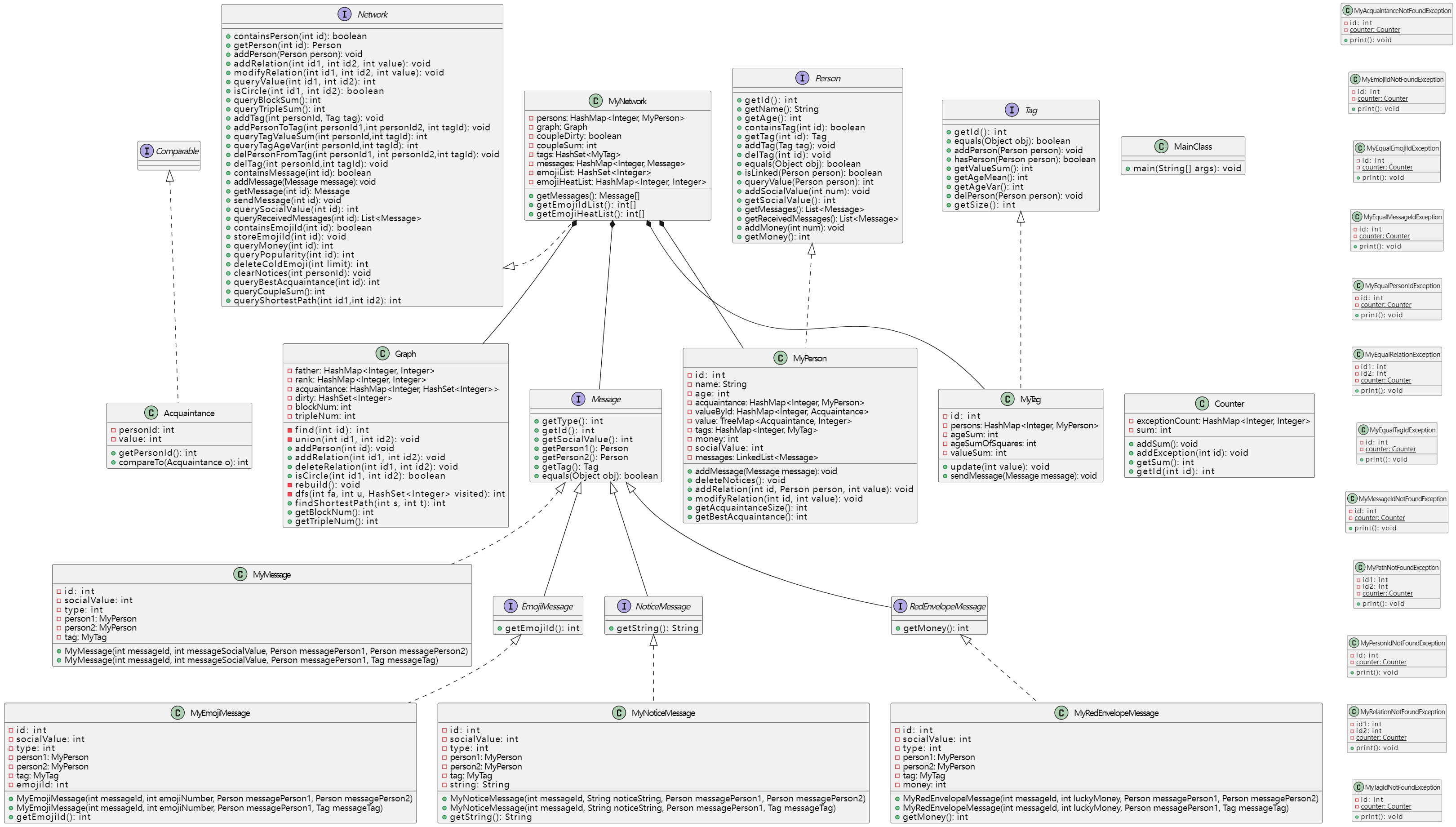
虽然基本上规格都由 $\mathcal{JML}$ 给出了，但它只是定义了方法或者接口的外部可感知行为及其约束，以及需要管理的数据所要满足的要求，实际编写代码时，我们需要灵活使用不同算法和数据结构，才能在保证性能的同时达成想要的效果。

在本单元作业实现中，我新建了Graph类，使用邻接表存储信息，将绝大部分维护信息的工作从Network类中分出来，Network只负责实现各种业务的接口。

其他的部分如Tag、Person、Message和异常类则由 $\mathcal{JML}$ 规定好了，总体结构没有什么特别的地方。

时间复杂度分析

本单元要求维护一张关系图（初始为空），并支持修改和查询操作（指令数 $N \leqslant 10^4$ ）。为了在时限内通过所有数据，我们需要保证每种操作的时间复杂度最多为 $O(N)$ ，在保证正确性的基础上再尝试进行复杂度优化或常数优化。

首先是最基本的add relation和modify relation，其实可以 $O(1)$ 实现，但是为了避免queryTripleSum、queryTagValueSum等操作的多重循环，需要在修改关系的时候对相关的信息进行维护，这样上述的查询操作就可以 $O(1)$ 完成。

//Graph.addRelation()
//维护三元环, deleteRelation时同理
if (acquaintance.get(id1).size() > acquaintance.get(id2).size()) {
//一点常数优化
    for (int o : acquaintance.get(id2)) {
        if (acquaintance.get(id1).contains(o)) {
            tripleNum++;
        }
    }
} else {
    for (int o : acquaintance.get(id1)) {
        if (acquaintance.get(id2).contains(o)) {
            tripleNum++;
        }
    }
}

对于TagValueSum的维护，与其费劲心思在Person类中维护信息，我选择了比较简单的实现，直接在Network中记录所有出现的Tag，修改所有满足条件的Tag即可。

//Tag.addPerson(), 删人同理
for (Person p : persons.values()) { valueSum += 2 * person.queryValue(p); }

//Network.addRelation(), modify同理
for (MyTag tag : tags) {
    if (tag.hasPerson(persons.get(id1)) && tag.hasPerson(persons.get(id2))) {
        tag.update(value);
    }
}

//Tag.java
public void update(int value) {
    valueSum += 2 * value;
}

对于queryTagAgeVar，计算方差原本是 $O(N)$ 的，不过可以在addPersonToTag、delPersonFromTag时 $O(1)$ 维护 $\sum Age,\sum Age^2$ ，然后就可以做到 $O(1)$ 查询方差。

对于queryShortestPath，实际就是01最短路，直接 $\mathcal{BFS}$ 即可（也可以双向，减小常数），复杂度 $O(E)$ （ $E$ 为边数小于指令数）

public int findShortestPath(int s, int t) {
    if (s == t) { return 0; }
    HashMap<Integer, Integer> dis = new HashMap<>();
    dis.put(s, 0);
    dis.put(t, 0);
    HashMap<Integer, Integer> flag = new HashMap<>();
    flag.put(s, 0);
    flag.put(t, 1);
    Queue<Integer> q = new LinkedList<>();//distance小的先进先出
    if (acquaintance.get(s).size() > acquaintance.get(t).size()) {//可能的常数优化（
        q.add(t);
        q.add(s);
    } else {
        q.add(s);
        q.add(t);
    }
    while (!q.isEmpty()) {
        int u = q.poll();
        int f = flag.get(u);
        for (int v : acquaintance.get(u)) {
            if (dis.containsKey(v)) {
                if (flag.get(v) != f) {//搜索交汇
                    return dis.get(u) + dis.get(v);
                } else { continue; }
            }
            dis.put(v, dis.get(u) + 1);
            flag.put(v, f);
            q.add(v);
        }
    }
    return 0;
}

对于queryBestAcquaintance，其实 $O(N)$ 查询也没问题，不过由于queryCoupleSum的存在，基本上要求必须在常数时间内实现qba。

当然我们还是可以再加人/删人的时候 $O(N)$ 维护最大值，不过我选择了用 $\mathcal{TreeMap}$ 去存acquaintance相关信息，这样就可以降低复杂度至 $O(logN)/O(1)$ 。

由于 $\mathcal{TreeMap}$ 只能以键值进行排序，研究了一阵子不得以我只能以一种很不优雅的方式自定义了比较器😕

//Person.java
private final HashMap<Integer, Acquaintance> valueById;
private final TreeMap<Acquaintance, Integer> value;

public int getBestAcquaintance() {
    return value.firstEntry().getKey().getPersonId();
}

//Acquaintance.java
public class Acquaintance implements Comparable<Acquaintance> {
    private final int personId;
    private final int value;
    
    //...
    
    @Override
    public int compareTo(Acquaintance o) {
        if (value == o.value) {
            return Integer.compare(personId, o.personId);
        }
        return Integer.compare(o.value, value);
    }
}

其他指令基本上根据 $\mathcal{JML}$ 来就好，除了维护整张图关系的并查集，基本没有使用算法和数据结构进行优化的必要了。

并查集的延迟重建

本来我们可以使用路径压缩+启发式合并的并查集，做到每个关系修改和查询（isCircle）操作的平均时间为 $O(\alpha(N))$ （可以认为是很小的常数），同时queryBlockSum也可以 $O(1)$ 维护和查询。

不过有了modifyRelation删边操作，我们不得不在某些时候对并查集进行重建。

如果是每次判断需要删边时无脑全部重建，则很大可能会被卡烂掉（常数+评测机波动）

每次删边时部分重建，常数小了很多，不过很多时候不太必要（因为只有查询的时候才需要准确的BlockSum和isCircle）

//Graph.deleteRelation()
HashSet<Integer> visited = new Hashset<>();
father.put(id1, id1);
dfs(id1, id1, visited);
rank.put(id1, visited.size());
if (!visited.contains(id2)) {
    father.put(id2, id2);
    visited.clear();
    dfs(id2, id2, visited);
    rank.put(id2, visited.size());
}


//dfs
private dfs(int fa, int u, Hashset<Integer> visited) {
    visited.add(u);
    for (int v : acquaintance.get(u)) {
        if (!visited.contains(v)) {
            father.put(v, fa);
            rank.put(v, 1);
            dfs(fa, v, visited);
        }
    }
}

或者删边时设置脏位，需要查询时才重建并查集。不过这样的话，当修改和查询指令轮流到来时，这个方法会和1一样拉（因为会无脑全部重建）

结合以上思路我们可以设计一种带有精确脏位的并查集（思路来自讨论区jhz同学的分享）

具体来说，我们可以将原来标记整个图的脏位扩展为对每个联通块进行脏位标记，设置dirty为所有被删边操作污染的父节点

private final HashSet<Integer> dirty;

//Graph.deleteRelation()
int f = find(id1);
if (!dirty.contains(f)) {//不要重复了
    dirty.add(f);
    blockNum--;//先不考虑这个联通块的贡献
}
/*
	这个行为的意义是，进行了此次删边操作后，以f为父节点的联通块内的具体情况我们将不得而知，
	这个联通块内所有点的关系信息是“不确定”的，需要查询时我们就对这些点进行关系的重建
*/

重建的步骤为

若dirty不为空，则所有的父节点在dirty中的点是我们需要重建的点
从需要重建的点的集合中开始 $\mathcal{DFS}$ ，重建这部分并查集

private void rebuild() {
    if (!dirty.isEmpty()) {
        HashSet<Integer> needToBuild = new HashSet<>();
        for (int id : acquaintance.keySet()) {
            /*
            	一定要先找出所有要重建的点，而不能边重建边判断哪些点需要重建，
            	因为重建到一半的并查集的信息是“不稳定的”，
            	重建的过程中再去判断点是否要重建，就可能会漏掉部分点
            */
            if (dirty.contains(find(id))) {//父节点被标记
                needToBuild.add(id);
            }
        }
        HashSet<Integer> visited = new HashSet<>();
        for (int id : needToBuild) {
            if (!visited.contains(id)) {
                father.put(id, id);
                rank.put(id, dfs(id, id, visited));
                blockNum++;//有了一个联通块
            }
        }
        dirty.clear();
    }
}

private int dfs(int fa, int u, HashSet<Integer> visited) {
    visited.add(u);
    int cnt = 1;
    for (int v : acquaintance.get(u)) {
        if (!visited.contains(v)) {
            father.put(v, fa);
            rank.put(v, 1);
            cnt += dfs(fa, v, visited);
        }
    }
    return cnt;//返回联通块的大小
}

这是对于查询操作，queryBlockSum我们需要调用rebuild。

而对于isCircle，需要分以下几种情况讨论：

若!dirty.contains(f1) && !dirty.contains(f2)，则这两个联通块都未被污染，正常判断即可
若dirty.contains(f1) && dirty.contains(f2)，则此时对我们来说这两个联通块的状态是“薛定谔的”，需要重建
而若两个父亲只有一个脏位被标记，这是我们立即得出被查询的两个点是不联通的（因为显然这两个点父节点不一样）

剩下的就是正常的并查集的相关操作，不过最后还有一点需要注意~~血泪教训~~：

就是并查集合并的时候，需要优先将没有脏位的父节点合并到有脏位的父节点，否则这个联通块的脏位信息是不准确的

private void union(int id1, int id2) {
    int fa1 = find(id1);
    int fa2 = find(id2);
    if (fa1 != fa2) {
        if (dirty.contains(fa1) == dirty.contains(fa2)) {
            //启发式合并
            if (rank.get(fa1) > rank.get(fa2)) {
                father.put(fa2, fa1);
                rank.put(fa1, rank.get(fa1) + rank.get(fa2));
            } else {
                father.put(fa1, fa2);
                rank.put(fa2, rank.get(fa2) + rank.get(fa1));
            }
        } else if (dirty.contains(fa1)) {
            father.put(fa2, fa1);
            rank.put(fa1, rank.get(fa1) + rank.get(fa2));
        } else {
            father.put(fa1, fa2);
            rank.put(fa2, rank.get(fa2) + rank.get(fa1));
        }
        blockNum--;
    }
}

由于重建操作只在需要的时候进行，并且我们精确了重建的点的范围，无论对于什么数据，这种方法相较于前面几种都是只优不劣的。

容器类的选择和轮子的使用

由于本单元维护的是一个社交网络，每个对象的 $\mathcal{Id}$ 是独一无二的，且取值范围是 $\mathcal{Int}$ ，所以我们可以很自然地想到用使用HashMap，建立 $\mathcal{Id}$ 到各种属性/对象的映射。

而对于其他一些不需要这样的映射的对象的集合，则基本来说HashSet是较优的选择（因为对象不重复且可以 $O(1)$ 使用contains）。

然后对于getReceivedMessages，要求返回前 $5$ 个Message，所以不能内部无序的HashMap或HashSet。经过查阅资料和参考讨论区czx同学的思路分享，最终选择了基于链表的LinkedList来存储Messages。

具体操作为：添加Message时使用addFirst方法，删除时使用removeIf方法。

//Person.java
public void addMessage(Message message) {
    messages.addFirst(message);
}

public void deleteNotices() {
    messages.removeIf(message -> message instanceof MyNoticeMessage);
}

对于删除上述容器中的特定元素操作，一般而言，我们都会采用迭代器的形式去遍历

Iterator<E> it = collection.iterator();
while (it.hasNext) {
    E item = it.next;
    if (check(item)) {
        it.remove();
        //...
    }
}

但其实Collection接口定义了方法removeIf，我们需要实现的删除操作正可以用这个现成的方法来实现，而且看起来十分优雅。下面是removeIf的相关用法。

1	boolean removeIf(Predicate<? super E> filter);

其中，Predicate是函数式接口，用于表示一个断言，该函数接受一个参数并返回布尔值。在 removeIf 方法中，传入一个 Predicate 类型的参数，表示要移除的元素需要满足的条件。若删除成功则返回真。

可以使用 $\mathcal{Lambda}$ 表达式（允许把函数作为一个方法的参数）定义过滤条件

/*
	(parameters) -> expression
	或
	(parameters) -> { statement; }
*/

//比如删除所有的NoticeMessage
messages.removeIf(message -> message instanceof MyNoticeMessage);

//删除emojiList中emojiHeatList不存在的key
emojiList.removeIf(emoji -> !emojiHeatList.containsKey(emoji));

//删除emojiList中emojiHeatList存在的key（方法引用）
emojiList.removeIf(emojiHeatList::containsKey);

自定义一个实现Predicate接口的类来定义过滤条件

Collection<E> collection = new ArrayList();
collection.removeIf(new Predicate<E>() {
    @override
    public boolean test(...) {
        //...
    }
});

性能与bug修复

本单元一个最大的优化就是实现了并查集的延迟重建功能。

其实hw9的时候我想着因为有删边，不管怎样处理都要 $O(N)$ ，所以直接无脑重建（想的是反正最多是 $O(E^2)$ 而且时限 $10s$ ），但是由于load_network指令的存在，第一次作业数据范围给的就显得有点大了（虽然后面改小了，虽然强测 $T$ 掉的点打赢复活赛了）。所以后面两次作业改成了延迟重建的并查集。

然后就是hw10强测和互测的bug，其实挺不应该的，queryTagValueSum直接写的双重循环计算。~~但是我这么做也是有理由的，你听我慢慢狡辩~~。首先是当时维护 $ValueSum$ 的过程出了一点麻烦，一直没搞清楚哪里出了问题，并且由于 $\mathcal{JUnit}$ 中测也只有两次机会了；然后翻了翻hw9打赢复活赛的点，发现只给了一千条左右的指令，想着课程组还挺良心的嘛，数据确实有梯度😃。

总之最后还是懒了，没改原来的双重循环，结果强测（一万条指令）和互测人直接被卡晕掉了。~~这波被课程组狠狠背刺了。~~

hw11互测出了bug，就是上文提到的十分隐蔽的关于延迟重建的并查集的合并细节，收回伏笔了属于是。

对于规格与实现分离的理解，其实已经体现在架构设计中了。

设计一些规格之外的方法，辅助业务代码的实现；而这其中又可以灵活采用合适的算法、数据结构等。

总的来说，这单元做得不是很好吧，本来轻松可以避免的bug没有去做，感觉经历了上个单元电梯的拷打、两次作业费尽心思写影子电梯但最终都没有做到完美，和这单元又碰上 $\mathcal{JML}$ ，整个人有点懒了。

但是不管怎么说， $\mathcal{OO}$ 课程要进入最后一个单元了， $debug$ 能力（指狼狈地修复bug时）还是一如既往地在线。

JUnit测试

上学期 $\mathcal{OOP}$ 的时候已经品尝过了 $\mathcal{JUnit}$ ，当时感觉是真的鸡肋，也不好写。

这单元学了 $\mathcal{JML}$ 和怎么对规格进行测试，（~~虽然可能是装模作样地在测试规格~~）感觉又还行了。

主要还是模仿实验课上的代码，使用Parameters生成数据搭建 $\mathcal{JUnit}$ 测试框架，如：

@RunWith(Parameterized.class)
public class NetworkTest{
    private final MyNetwork myNetwork;
    
    public MyNetworkTest(MyNetwork myNetwork) { this.myNetwork = myNetwork; }
    
    @Parameters
    public static Collection prepareData() {
        int testNum = 10;
        Object[][] objects = new Object[testNum][];
        for (int k = 0; k < testNum; ++k) {
            //do something, such as generating network by implementation functions
        }
        return Arrays.asList(objects);
    }
    
    @Test
    public void oneFuction() {
        /*
        	测试对应方法是否满足规格要求
        	如pure, ensures, signals等
        */
    }
}