前言

随着第三次作业的强测结果公布，这一单元的学习也接近了尾声。从开始的迷茫和手足无措，到最后可以拿出一份层次清晰、结构完整代码，我开始对作业所要求的层次化设计思想有了一定感觉，也体会到编写代码时各个类之间做到有效协同、职责分派之后带来的高效和美观。这些也离不开许多同学在讨论区的想法分享和往年学长学姐的经验总结。下面我将以我的学习总结和心得体会为第一单元的学习画上一个句号。

程序架构分析

得益于课程组大力提倡的递归下降法和实验课提供的demo，以及同学在讨论区的各式各样的想法分享，我能够在开始时就采用一个比较优秀的架构，所以本单元迭代过程中基本没有大的重构。因此关于代码架构的分析就以hw3的代码为主了。

整体架构

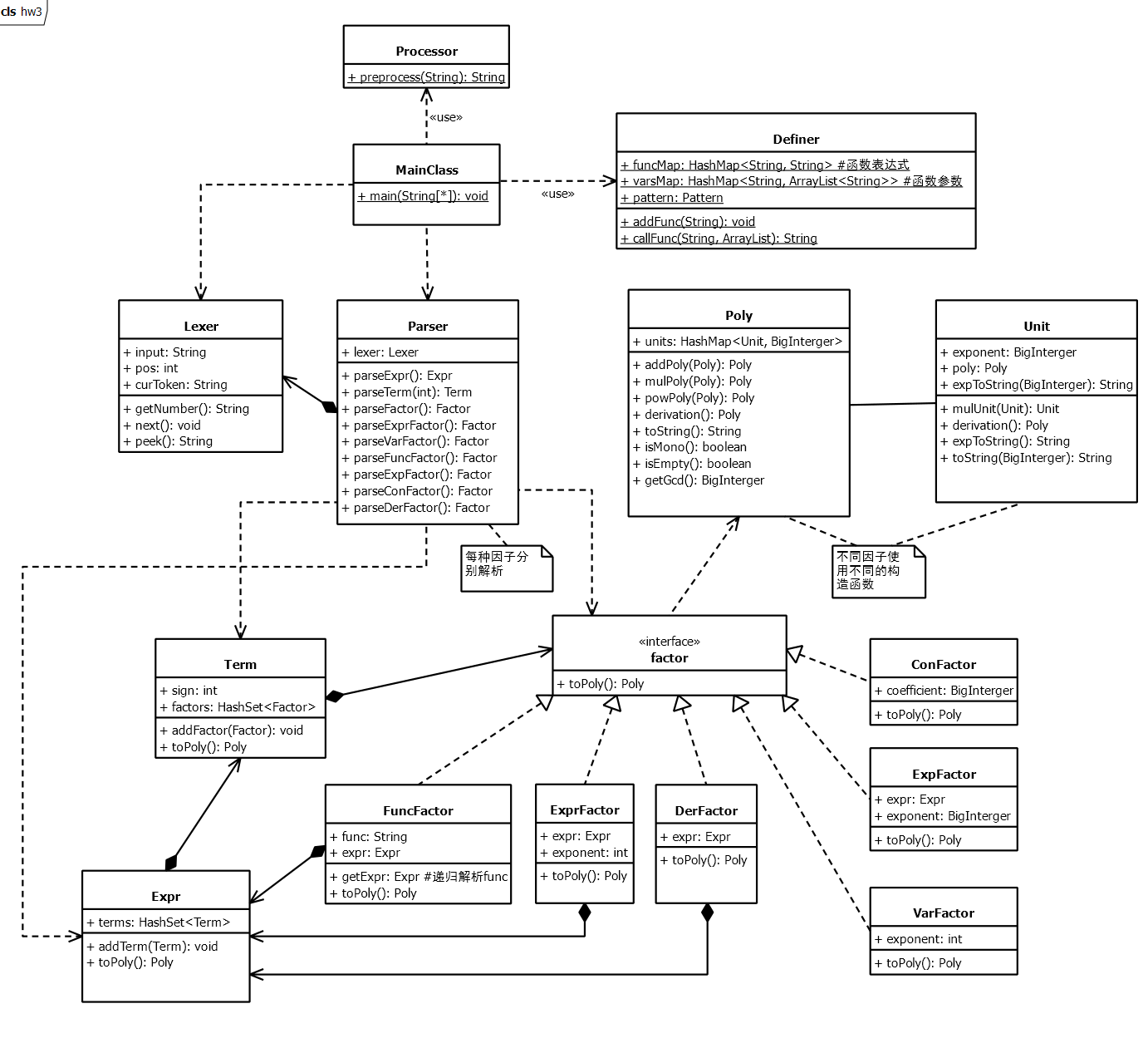
首先根据题目的形式化表述，可以很自然地建出Expr -> Term -> Factor这样一个结构，而其中Factor又可以根据不同情况建立不同子类。将读入经过预处理之后，在使用递归下降的方法就可以清晰地将表达式解析开来。

接下来对于表达式的展开主要借鉴了zyt同学的思路，从由若干基本单元组成的多项式的输出结果出发，考虑将从原始表达式解析出来的东西化归为统一的形式——即Poly类，然后在此类中依据题目要求定义不同运算方法。同时，将Factor定义为包含toPoly()接口的抽象类，也就可以沿着上述的结构递归地返回展开结果。最后在Poly类中重写toString即可进行结果的输出。

另外，关于自定义函数的处理，我采用了字符串替换的形式，将使用parseFactor方法得到的实参代入形成新的表达式，然后调用parseExpr即可。不用额外去考虑函数的嵌套，因为这样的递归结构已经就可以处理这个问题（就如同处理嵌套的括号一样）。

而对于导数的处理，我没有递归地返回各类因子求导结果，而是直接把求导看成一种运算，最后通过toPoly得到标准形式后再调用一次Poly中的求导方法即可。

具体的UML图如下

UML图

代码规模分析

采用插件Statistic

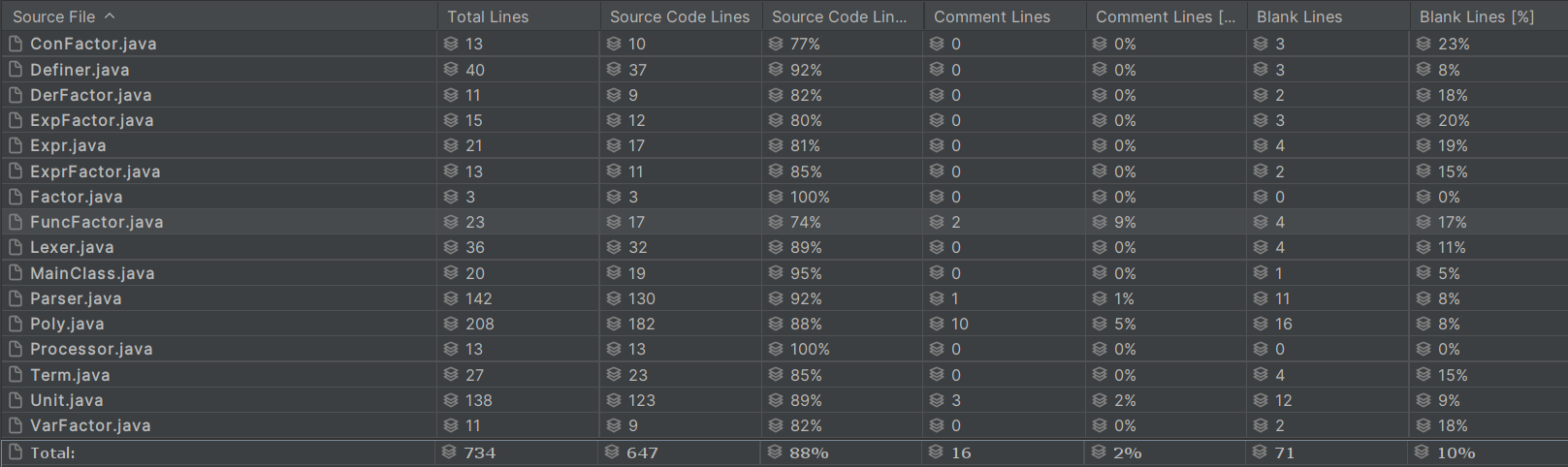
可以看到总体的规模并不大，除去用于优化输出结果的部分，整份代码的实际行数也就不到600行。

其中多项式Poly类和基础单元Unit类占据了主要的部分，这也符合上述代码架构的逻辑。

代码复杂度分析

采用插件MetricsReloaded分析，其中所用度量标准如下：

  • CogC: 方法的认知复杂度。
  • ev(G)：方法的基本圈复杂度，衡量程序非结构化程度，表示真正增加程序路径数目的条件分支。
  • iv(G)：方法的设计复杂度，设计复杂度高意味模块耦合度高，这将导致模块难于隔离、维护和复用。
  • v(G)：方法的独立路径的条数。
  • OCavg：类的平均操作复杂度
  • OCmax：类的最大操作复杂度
  • WMC：类的加权方法复杂度

其中超标的部分用粗体标出。

method CogC ev(G) iv(G) v(G)
ConFactor.ConFactor(BigInteger) 0 1 1 1
ConFactor.toPoly() 0 1 1 1
Definer.addFunc(String) 3 1 3 3
Definer.callFunc(String, ArrayList<Factor>) 1 1 2 2
DerFactor.DerFactor(Expr) 0 1 1 1
DerFactor.toPoly() 0 1 1 1
ExpFactor.ExpFactor(BigInteger, Expr) 0 1 1 1
ExpFactor.toPoly() 0 1 1 1
Expr.Expr() 0 1 1 1
Expr.addTerm(Term) 0 1 1 1
Expr.toPoly() 1 1 2 2
ExprFactor.ExprFactor(Expr, int) 0 1 1 1
ExprFactor.toPoly() 0 1 1 1
FuncFactor.FuncFactor(String, ArrayList<Factor>) 0 1 1 1
FuncFactor.getExpr() 0 1 1 1
FuncFactor.toPoly() 0 1 1 1
Lexer.Lexer(String) 0 1 1 1
Lexer.getNumber() 2 1 3 3
Lexer.next() 3 2 2 3
Lexer.peek() 0 1 1 1
MainClass.main(String[]) 1 1 2 2
Parser.Parser(Lexer) 0 1 1 1
Parser.parseConFactor() 2 1 3 3
Parser.parseDerFactor() 0 1 1 1
Parser.parseExpFactor() 1 1 2 2
Parser.parseExpr() 7 1 6 6
Parser.parseExprFactor() 1 1 2 2
Parser.parseFactor() 7 6 8 8
Parser.parseFuncFactor() 1 1 2 2
Parser.parseTerm(int) 3 1 3 3
Parser.parseVarFactor() 1 1 2 2
Poly.Poly() 0 1 1 1
Poly.Poly(BigInteger) 0 1 1 1
Poly.Poly(BigInteger, BigInteger) 0 1 1 1
Poly.Poly(Poly, BigInteger) 0 1 1 1
Poly.Poly(int) 0 1 1 1
Poly.addPoly(Poly) 8 1 6 6
Poly.derivation() 1 1 2 2
Poly.equals(Object) 3 3 2 4
Poly.getGcd() 4 1 3 3
Poly.hashCode() 0 1 1 1
Poly.isEmpty() 0 1 1 1
Poly.isMono(BigInteger) 2 3 2 3
Poly.mulPoly(Poly) 9 1 6 6
Poly.powPoly(int) 6 1 4 4
Poly.toString(BigInteger) 16 3 9 9
Processor.preprocess(String) 2 1 5 5
Term.Term(int) 0 1 1 1
Term.addFactor(Factor) 0 1 1 1
Term.toPoly() 2 1 3 3
Unit.Unit() 0 1 1 1
Unit.Unit(BigInteger) 0 1 1 1
Unit.Unit(BigInteger, Poly) 0 1 1 1
Unit.Unit(Poly) 0 1 1 1
Unit.derivation(BigInteger) 4 2 3 3
Unit.equals(Object) 3 3 2 4
Unit.expToString() 7 1 3 4
Unit.hashCode() 0 1 1 1
Unit.isMono(BigInteger, BigInteger) 6 4 4 7
Unit.mulUnit(Unit) 0 1 1 1
Unit.toString(BigInteger) 24 1 13 13
VarFactor.VarFactor(int) 0 1 1 1
VarFactor.toPoly() 0 1 1 1
Total 131 81 143 153
Average 2.08 1.29 2.27 2.43
class OCavg OCmax WMC
ConFactor 1.00 1 2
Definer 2.50 3 5
DerFactor 1.00 1 2
ExpFactor 1.00 1 2
Expr 1.33 2 4
ExprFactor 1.00 1 2
FuncFactor 1.00 1 3
Lexer 1.75 3 7
MainClass 2.00 2 2
Parser 2.70 6 27
Poly 2.87 9 43
Processor 2.00 2 2
Term 1.67 3 5
Unit 3.00 13 33
VarFactor 1.00 1 2
Total 141
Average 2.24 3.27 9.40

可以看到，复杂度的情况基本符合预期。两个类中重写的toString方法加入了对优化的处理和判断，从而导致复杂度飙升；而isMono也是用作优化处理，判断某个多项式是否为基本单元。另外，由于parseFactor中对不同因子分别单独处理，使用了大量串行分支判断，此处的优化可以学习zpy同学的总结。

架构设计体验

从0到1

俗话说，万事开头难。由于第一周刚经历了假期，上学期先导课学习的内容有不少遗忘，且对于第一份作业眼花缭乱的形式化表述有些迷糊，我经历了好几天的迷茫。虽然通过不断地去看训练项目、实验课的代码和oolen上对递归下降的讲解，大概明白了递归下降的思想，但我还是感觉下不了手。凭借递归下降在给的demo上修修改改固然就能完成比较简单的第一次作业，但我还是没构思好该用什么样的一个架构，怎样去处理解析后得到的不同形式的部分，害怕搞个大的等到以后迭代时不得不remake。

很快就到了周五，而我还没开始敲一行代码。很感谢讨论区同学的无私分享，在看完zyt同学发的帖后，我才算是有了一点头绪和对层次化的理解，尝试去将他展现出来的思路实现出来。

当我写完各个类的属性方法，补完预处理和解析的部分，整份代码居然就可以“神奇”地跑出结果来了（虽然由于解析部分的bug没有全过样例）。恍惚间，我开始体会到各个类之间“有效协同，职责分派”的魔力，每个类通过其管理的对象提供的行为来完成任务，每个方法立足类的属性数据来规划行为，从而将原本复杂的任务目标拆解成逻辑清晰、结构清楚的形式。同时，我也开始逐渐接受递归处理在面向对象过程中实现的作用。

不过，由于第一次作业的基本单元较为简单a*x^n， 所以最开始时我没有建立单独的类去管理，直接将系数-指数这一键值对存入Poly中的map中。

对于预处理，我采用了以下的方法并同时处理了前导零（互测过后我才发现这是多余的，同时预处理我也是直接写在main中的）。

1
2
3
4
5
6
7
8
input = input.replaceAll("[ \t]", "");
while (input.contains("+-") || input.contains("-+") ||
        input.contains("++") || input.contains("--")) {
    input = input.replaceAll("\\+-|-\\+", "-");
    input = input.replaceAll("\\+\\+|--", "+");
}
input = input.replaceAll("\\^\\+", "^");
input = input.replaceAll("\\*\\+", "*");

此时字符串中没有连续的正负号了，只剩开头和(后的正负号以及*后的负号需要处理。于是在parseExpr和parseTerm中加入处理，并在Term中增加了属性sign表示正负号，若为负，递归生成多项式的时候乘一项-1,即可解决这一问题。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
//parseExpr
Expr expr = new Expr();
int sign = 1;
if (lexer.peek().equals("-")) {
    sign = -1;
    lexer.next();
} else if (lexer.peek().equals("+")) {
    lexer.next();
}
expr.addTerm(parseTerm(sign));
while (lexer.peek().equals("+") || lexer.peek().equals("-")) {
    ...
}
return expr;

//parseTerm
...
while (lexer.peek().equals("*")) {
    lexer.next();
    if (lexer.peek().equals("-")) {
        term.addFactor(new ConFactor(BigInteger.valueOf(-1)));
        lexer.next();
    }
    term.addFactor(parseFactor());
}
...
    
//Term.toPoly()
Poly poly = new Poly(BigInteger.valueOf(1));
for (Factor factor : factors) {
    poly = poly.mulPoly(factor.toPoly());
}
if (sign == -1) {
    poly = poly.mulPoly(new Poly(BigInteger.valueOf(-1)));
}
return poly;

从第一次作业到第二次作业

这一次作业新增了指数函数、自定义函数和嵌套的括号

这次作业是很痛苦的一次迭代，斟酌了很久怎么调整架构，debug也de到了昏天黑地。

首先是新增的指数函数使得之前基础单元需要改动，于是对于怎样定义新增类Unit的属性和处理它和Poly的关系，我又陷入了反复否定自己的思考。最后将信将疑地还是使用了递归定义的形式，并在敲下一行行代码后逐渐肯定了这一结构。

1
2
3
4
5
6
7
8
9
10
public class Poly {
    private final HashMap<Unit, BigInteger> units;
    ...
}

public class Unit {
    private final BigInteger exponent;
    private final Poly poly;
    ...
}

接着，为了进行同类项的合并，对这两个类重写了equals和hashcode方法：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
//Unit
public boolean equals(Object o) {
    if (this == o) {
        return true;
    }
    if (!(o instanceof Unit)) {
        return false;
    }
    Unit unit = (Unit) o;
    return this.exponent.equals(unit.exponent) && this.poly.equals(unit.poly);
}

public int hashCode() {
    return Objects.hash(this.exponent, this.poly);
}
//Poly
public boolean equals(Object o) {
    if (this == o) {
        return true;
    }
    if (o == null || getClass() != o.getClass()) {
        return false;
    }
    Poly poly = (Poly) o;
    return this.units.entrySet().equals(poly.units.entrySet());
}

public int hashCode() {
    return Objects.hash(this.units.entrySet());
}

值得一提的是Poly中需要用units的键值对entrySet()而不是keySet()或者valueSet()。在这个地方de了好久，当时还以为是深浅拷贝出了问题。

有了以上基础之后，接着顺便把Poly中的方法重新写了一遍（包括构造函数和运算方法（这应该不算大的重构把）），也特别注意了第一次没在意的深浅拷贝问题。

然后是对自定义函数的处理。因为形式化表述中看到参数也是因子，所以仿照表达式因子的处理方法，于是采用了字符串替换的递归处理方式，将展开得到的参数因子带入，得到新的表达式，解析并返回结果。

函数定义式的拆解使用了正则表达式：

1
2
3
4
private static final Pattern pattern = Pattern.compile("([A-Za-z]+)\\(([A-Za-z,]+)\\)=(.+)");
//存储变量和函数式子
private static final HashMap<String, String> funcMap = new HashMap<>();
private static final HashMap<String, ArrayList<String>> varsMap = new HashMap<>();

另外有几个需要注意的点，1）将式子中的变量x换成_x的形式，避免后续替换时对exp造成影响。2）带入参数需要在左右添加括号。（血泪教训）

最后将预处理的过程写成了一个静态类，保留了一个清清爽爽的main函数

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
public static void main(String[] args) {
    Scanner scanner = new Scanner(System.in);
    int n = Integer.parseInt(scanner.nextLine());
    String input;
    for (int i = 0; i < n; ++i) {
        input = Processor.preprocess(scanner.nextLine());
        Definer.addFunc(input);
    }
    input = Processor.preprocess(scanner.nextLine());
    Lexer lexer = new Lexer(input);
    Parser parser = new Parser(lexer);
    Expr expr = parser.parseExpr();
    String ans = expr.toPoly().toString();
    if (ans.isEmpty()) {
        ans = "0";
    }
    System.out.println(ans);
}

总之，这次迭代让我对整个架构有了更深的理解和体会。

从第二次作业到第三次作业

这次作业新增了求导因子dx()，以及函数定义时可以调用其他函数。

经历了上次迭代的痛苦，这次作业就可以说是“轻舟已过万重山”了。之前的架构已经比较完善了，而字符串替换的方法可以轻松解决自定义函数的调用。同时如果采用最后才进行一次求导的方法，求导因子也可以在Poly和Unit中增加对应的运算方法，从而得到解决。

[a∗xn∗exp⁡(poly)]′=(a∗n∗xn−1+a∗xn∗poly′)∗exp⁡(poly)[a*x^n*\exp(poly)]' = (a*n*x^{n-1}+a*x^n*poly')*\exp(poly) 

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
//递归求导
//Poly
public Poly derivation() {
    Poly retPoly = new Poly();
    Iterator it = this.units.keySet().iterator();
    while (it.hasNext()) {
        Unit unit = (Unit) it.next();
        retPoly = retPoly.addPoly(unit.derivation(this.units.get(unit)));
    }
    return retPoly;
}
//Unit
public Poly derivation(BigInteger coefficient) {
    if (this.poly.isEmpty()) {
        BigInteger newExp = this.exponent;
        if (!newExp.equals(BigInteger.valueOf(0))) {
            newExp = newExp.add(BigInteger.valueOf(-1));
        }
        BigInteger newCoe = coefficient.multiply(this.exponent);
        return new Poly(newCoe, newExp);
    } else {
        Poly poly = new Poly(coefficient, this.exponent);
        return new Poly(this.poly, BigInteger.valueOf(1)).mulPoly(
                poly.derivation().addPoly(poly.mulPoly(this.poly.derivation())));
    }
}

此外，这次迭代增加了对exp()提取最大公因数的优化。需要注意的是不能直接在toString()中直接对要输出的系数进行修改。

bug分析

本单元三次作业在中测、强测、互测中均未出现bug，算是安全过关了。这也要感谢大佬们搭建的评测机，尤其是第二次作业我好不容易终于写完了所有代码以后，帮我找到了解析过程中和处理自定义函数时的bug。

感觉自己的debug能力又提升了不少，大致谈一谈debug策略吧。

  • 首先是根据初始的数据（可能很大且复杂），尝试不断去除其中的部分，慢慢定位可以导致错误的部分
  • 然后通过输出中间变量和各种调试语句去发现bug（因为IDEA的调试我觉得实在是难用且费眼费脑）
  • 总之，定位了大概出错的区域，基本上就能将bug解决

其实大部分还是写的过程中不细心导致的，除了集中注意力，也需要我们对自己的代码和架构了然于胸。

hack分析

第一次作业由于比较基础简单，所以房内并未出现刀人情况。

第二次作业根据debug的经验和评测姬发现了房内同学的两个bug

1
2
3
4
5
6
7
8
9
10
2
f(x) = exp(x^+02)
h(y , z , x) = ++exp(x)^+3
++h(        ( f(x) ), ( f(x) ), f(x))
//处理实参时没有注意因子定义，导致碰到括号时出错
    
1
f(x,y)=-x^0-2*exp(x)*exp(y)
f(exp(1),0)*exp(-1)
//优化exp(0)出了问题

第三次作业仍然是测出了以为同学不能处理好exp(0)的问题

1
2
3
1
g(z) = ++exp(0)+-1
exp(g(x) )

总之，如果想要成功出刀的话，需要对题目的要求有清楚的理解和一定的hack策略，比如：

  • 根据评测机数据构造能通过cost限制的同质bug数据
  • 多进行corner case的测试
  • 因为递归较多，可以进行合理范围内的压力测试

在第三次作业时，因为没有利用好cost的限制，虽然有构造压力测试样例的想法，但最后因为不知道哪里触发了互测数据限制，浅尝辄止，浪费了出刀的好机会。这也是以后互测我需要注意改进的地方吧。

优化分析

第一次作业基本没什么优化的空间，只有一个（基本的合并同类项就不提了）——尽量保证Expr的第一项系数为正（可以少一个符号）。

第二次作业引入指数函数后，事情便走向了不可控的境地。通过同学们的讨论发现基本没法做到最优，再加上那一周的迭代实在太过艰辛，于是放弃了这个方向的优化，只求能先保证正确性。于是只对exp的系数是否为正负1和指数是否为0，以及指数部分是否为不用添加括号的单项式（因子），进行了优化。

第三次作业虽然没有去搞各种复杂的拆分，但增加了提取最大公因数的优化，不过优得不是很化——没有把Gcdk(1⩽k⩽9)\frac{Gcd}{k}(1 \leqslant k \leqslant 9)的情况都比较一遍，导致强测有一个点的性能分出现了一点点的负优化。

总之，虽然第三次做优化的时候很可惜为什么第二次不加上最大公约数的优化（那样就又可以多一点分了），但实际上做优化的时候又对优化带来的对正确性的bug de了好久，而且第二次作业de完bug感觉整个人的精神已经是强弩之末了，说不定反而会弄巧成拙。包括第三次作业做的优化，我自知肯定是卷不过那些优化仙人的（感觉也没必要），于是就对性价比最大的一部分进行了优化，这也算是一种trade-off吧。

心得体会

对于我自身而言，第一单元的学习也带给了我很多关于面向对象构造的思考（其中一位同学发的帖也很令人深思 命令-查询分离原则），对于如何将复杂问题进行层次分解和抽象，在之后的单元我还需要进行更多的学习和思考。

另外，我也需要注意对已有轮子的学习和使用，从而更多关注架构的设计。如本单元作业中，最开始对BigInterger不熟悉，合并同类项的Merge方法，优化时的处理有compareTo……

最后感谢上学期的oopre确实给我打下了一定的基础（否则不敢想我面对Unit 1的冲击会有多狼狈），也很感谢分享经验和搭建评测机的同学的帮助。

未来方向

对于课程设计，我还是觉得对exp的拆分优化这些，这感觉已经不能算是化简了，而且以大量的运行时间换来了这样的长度的减少，感觉没有体现出性能二字意义何在。优化仙人们确实很厉害，但这部分的工作不是学好OO这门课必要的。