绪论
算法
计算 = 信息处理 = 借助某种工具,遵照一定规则,以明确而机械的形式进行
计算模型 = 计算机 = 信息处理工具
算法,是指基于特定的计算模型,旨在解决某一信息处理问题的指令序列。
有穷性:任意算法都应在执行有限次基本操作之后终止并给出输出
正确性:所给的输出应能符合由问题本身在事先确定的条件
健壮性:能处理各种极端的输入实例
可计算性
效率
起泡排序
1 2 3 4 5 6 7 8 9 10 11 12 13 void bubblesort1A (int A[], int n) bool sorted = false ; while (!sorted) { sorted = true ; for (int i = 1 ; i < n; i++) { if (A[i - 1 ] > A[i]) { swap (A[i - 1 ], A[i]); sorted = false ; } } n--; } }
复杂度度量
问题实例的规模,往往是决定计算成本的最主要因素。通常,规模接近,计算成本也接近;规模扩大,计算成本亦上升。
T A ( n ) T_A(n) T A ( n ) n n n T ( n ) T(n) T ( n )
取 T ( n ) = max { T ( P ) ∣ ∣ P ∣ = n } T(n) = \max\{T(P) | \left\vert P \right\vert = n\} T ( n ) = max { T ( P ) ∣ ∣ P ∣ = n }
计算模型
图灵机
部件
Tape:依次均匀地划分为单元格,各存有某一字符,初始均为“#”
Head
总是对准某一单元格,并可读取或改写其中的字符
每经过一个节拍,可转向左侧或右侧的邻格
State
TM 总是处于有限种状态中的某一种
每经过一个节拍可按照规则转向另一种状态
h = halt h = \text{halt} h = halt
Transition Function:( q , c ; d , L / R , p ) (q,c;d,L/R,p) ( q , c ; d , L / R , p )
若当前状态为 q q q c c c
将当前字符改写为 d d d
转向左/右侧邻格
转入 p p p
从启动至停机,所经历的节拍数目即可用以度量计算的成本
实例
将二进制非负整数加一
1 2 3 4 5 (<, 1 ; 0 , L, <) (<, 0 ; 1 , R, >) (<, #; 1 , R, >) (>, 0 ; 0 , R, >) (>, #; #, L, h/<)
RAM
组成
寄存器顺序编号,总数没有限制
可通过编号直接访问任意寄存器(call-by-rank)
每一基本操作只需常数时间
在这些模型中
算法的运行时间 ∝ \propto ∝
T ( n ) T(n) T ( n ) n n n
渐近复杂度
问题规模足够大之后,计算成本的增长趋势
big-O notation
T ( n ) = O ( f ( n ) ) ⟺ ∃ c > 0 s.t. T ( n ) < c ⋅ f ( n ) ∀ n ≫ 2 T(n) = O(f(n)) \iff \exist c > 0 \quad \text{s.t.} \quad T(n) < c \cdot f(n) \quad \forall n \gg 2 T ( n ) = O ( f ( n ) ) ⟺ ∃ c > 0 s.t. T ( n ) < c ⋅ f ( n ) ∀ n ≫ 2
由 O O O o o o
T ( n ) = o ( f ( n ) ) ⟺ ∀ c > 0 s.t. T ( n ) < c ⋅ f ( n ) ∀ n ≫ 2 T(n) = o(f(n)) \iff \forall c > 0 \quad \text{s.t.} \quad T(n) < c \cdot f(n) \quad \forall n \gg 2 T ( n ) = o ( f ( n ) ) ⟺ ∀ c > 0 s.t. T ( n ) < c ⋅ f ( n ) ∀ n ≫ 2 对于 f ( n ) = o ( g ( n ) ) f(n) = o(g(n)) f ( n ) = o ( g ( n ) ) lim n → ∞ f ( n ) g ( n ) = 0 \begin{aligned}\lim_{n \to \infty} \frac{f(n)}{g(n)} = 0\end{aligned} n → ∞ lim g ( n ) f ( n ) = 0
渐近符号也可以用来刻画算法的某个其他方面(如使用的空间数量)
其他记号
T ( n ) = Ω ( f ( n ) ) ⟺ ∃ c > 0 s.t. T ( n ) > c ⋅ f ( n ) ∀ n ≫ 2 T(n) = \Omega(f(n)) \iff \exist c > 0 \quad \text{s.t.} \quad T(n) > c \cdot f(n) \quad \forall n \gg 2 T ( n ) = Ω ( f ( n ) ) ⟺ ∃ c > 0 s.t. T ( n ) > c ⋅ f ( n ) ∀ n ≫ 2
T ( n ) = Θ ( f ( n ) ) ⟺ ∃ c 1 > c 2 > 0 s.t. c 1 ⋅ f ( n ) > T ( n ) > c 2 ⋅ f ( n ) ∀ n ≫ 2 T(n) = \Theta(f(n)) \iff \exist c_1 > c_2 > 0 \quad\text{s.t.} \quad c_1 \cdot f(n) > T(n) > c_2 \cdot f(n) \quad \forall n \gg 2 T ( n ) = Θ ( f ( n ) ) ⟺ ∃ c 1 > c 2 > 0 s.t. c 1 ⋅ f ( n ) > T ( n ) > c 2 ⋅ f ( n ) ∀ n ≫ 2
定义多重对数函数为 $\log^*(n) = \min{i\ge 0 : \log^{(i)}(n) \le 1 } $
由此可得 ∃ f ( n ) , lim n → ∞ f ( n ) = ∞ s.t. f ( n ) = Θ ( f ( log n ) ) \begin{aligned}\exist f(n), \lim_{n \to \infty} f(n) = \infty \quad \text{s.t.} \quad f(n) = \Theta(f(\log n))\end{aligned} ∃ f ( n ) , n → ∞ lim f ( n ) = ∞ s.t. f ( n ) = Θ ( f ( log n ) )
for (i = 1; i < n; i = (1 << i))
复杂度分析
O ( 1 ) O(1) O ( 1 )
通常 不含循环、分支、子程序调用仅需 O ( 1 ) O(1) O ( 1 )
C++等高级语言的基本指令,均等效于常数条 RAM 的基本指令
O ( log c n ) O(\log^c n) O ( log c n )
∀ c > 0 , log n = O ( n c ) \forall c > 0, \quad \log n = O(n^c) ∀ c > 0 , log n = O ( n c ) ln ( n ! ) ≈ ( n + 0.5 ) ln n − n \ln (n!) \approx (n + 0.5) \ln n - n ln ( n ! ) ≈ ( n + 0 . 5 ) ln n − n ∑ i = 1 n 1 i = ln n + γ + Θ ( 1 2 n ) , γ ≈ 0.577216 \begin{aligned}\sum_{i=1}^n \frac{1}{i} = \ln n + \gamma + \Theta(\frac{1}{2n}),\quad \gamma \approx 0.577216\end{aligned} i = 1 ∑ n i 1 = ln n + γ + Θ ( 2 n 1 ) , γ ≈ 0 . 5 7 7 2 1 6
O ( n c ) O(n^c) O ( n c )
a k ⋅ n k + a k − 1 ⋅ n k − 1 + ⋯ + a 1 ⋅ n + a 0 = O ( n k ) , a k > 0 a_k \cdot n^k + a_{k-1} \cdot n^{k - 1} + \cdots + a_1 \cdot n + a_0 = O(n^k), \quad a_k > 0 a k ⋅ n k + a k − 1 ⋅ n k − 1 + ⋯ + a 1 ⋅ n + a 0 = O ( n k ) , a k > 0
O ( 2 n ) O(2^n) O ( 2 n )
T ( n ) = O ( a n ) , a > 1 T(n) = O(a^n), \quad a > 1 T ( n ) = O ( a n ) , a > 1 从 O ( n c ) O(n^c) O ( n c ) O ( 2 n ) O(2^n) O ( 2 n )
Subset Sum → \rightarrow →
输入规模
待计算问题的输入规模,应严格定义为“用以描述输入所需的空间规模”。
封底估算
根据数据结构和算法的渐近复杂度,凭借在实际计算环境中积累的经验,针对计算过程主要部分进行的粗略估算。
迭代与递归
1 2 3 4 5 6 int sum (int A[], int n) if (n < 1 ) return 0 ; else return sum (A, n - 1 ) + A[n - 1 ]; }
线性递归
每一层次至多有一个实例,且它们构成一个线性的次序关系。
减而治之
为求解一个大规模的问题,可以
将其划分为两个子问题:其一平凡,另一规模缩减
分别求解子问题;再由子问题的解,得到原问题的解
递归每深入一层,待求解问题的规模都缩减一个常数,直至最终蜕化为平凡的小(简单)问题。
计算过程中出现过的所有递归实例,其所需时间总和,即为整体运行时间
空间复杂度:递归 深度 + 额外申请空间
尾递归和递归消除
在线性递归算法中,若递归调用在递归实例中恰好以 最后一步操作 的形式出现,则称作尾递归
属于尾递归形式的算法,均可简捷地转换为等效的迭代版本
1 2 3 4 5 6 7 8 9 void reverse (int *A, int n) if (n < 2 ) return ; swap (A[0 ], A[n - 1 ]); reverse (A + 1 , n - 2 ); } void reverse (int *A, int lo, int hi) while (lo < hi) swap (A[lo++], A[hi--]); }
分而治之
为求解一个大规模的问题,可以
将其划分为若干子问题(通常两个,且规模 大体相当 )
分别求解子问题;再由子问题的解,得到原问题的解
为使分治策略真正有效,需要保证
子问题之间相互独立
子问题划分和子解答合并能高效实现
主定理
分治策略对应的递推式,通常形如 T ( n ) = a ⋅ T ( n / b ) + O ( g ( n ) ) T(n) = a \cdot T(n / b) + O(g(n)) T ( n ) = a ⋅ T ( n / b ) + O ( g ( n ) )
原问题被分为 a a a n / b n/b n / b
任务的划分、解的合并,总共耗时 g ( n ) g(n) g ( n )
若 g ( n ) = Ω ( n log b a + ϵ ) g(n) = \Omega(n^{\log_b a + \epsilon}) g ( n ) = Ω ( n l o g b a + ϵ ) T ( n ) = Θ ( g ( n ) ) T(n) = \Theta(g(n)) T ( n ) = Θ ( g ( n ) )
ϵ > 0 \epsilon > 0 ϵ > 0 quickSelect(average case): T ( n ) = 1 ⋅ T ( n / 2 ) + O ( n ) = O ( n ) T(n) = 1 \cdot T(n / 2) + O(n) = O(n) T ( n ) = 1 ⋅ T ( n / 2 ) + O ( n ) = O ( n )
若 g ( n ) = O ( n log b a − ϵ ) g(n) = O(n^{\log_b a - \epsilon}) g ( n ) = O ( n l o g b a − ϵ ) T ( n ) = Θ ( n log b a ) T(n) = \Theta(n^{\log_b a}) T ( n ) = Θ ( n l o g b a )
large integer multiplicaton: T ( n ) = 3 ⋅ T ( n / 2 ) + O ( n ) = O ( n log 2 3 ) T(n) = 3 \cdot T(n / 2) + O(n) = O(n^{\log_2 3}) T ( n ) = 3 ⋅ T ( n / 2 ) + O ( n ) = O ( n l o g 2 3 )
若 g ( n ) = Θ ( n log b a ⋅ log k n ) g(n) = \Theta(n^{\log_b a} \cdot \log^k n) g ( n ) = Θ ( n l o g b a ⋅ log k n ) T ( n ) = { Θ ( n log b a ⋅ log k + 1 n ) , k > − 1 Θ ( n log b a ⋅ log log n ) , k = − 1 Θ ( n log b a ) , k < − 1 T(n) = \begin{cases} \Theta(n^{\log_b a} \cdot \log^{k + 1} n), & k > -1 \\ \Theta(n^{\log_b a} \cdot \log\log n), & k = - 1 \\ \Theta(n^{\log_b a}), & k < -1 \end{cases} T ( n ) = ⎩ ⎪ ⎪ ⎨ ⎪ ⎪ ⎧ Θ ( n l o g b a ⋅ log k + 1 n ) , Θ ( n l o g b a ⋅ log log n ) , Θ ( n l o g b a ) , k > − 1 k = − 1 k < − 1
STL mergesort: T ( n ) = 2 ⋅ T ( n / 2 ) + O ( n ⋅ log n ) = O ( n ⋅ log 2 n ) T(n) = 2 \cdot T(n / 2) + O(n \cdot \log n) = O(n \cdot \log^2 n) T ( n ) = 2 ⋅ T ( n / 2 ) + O ( n ⋅ log n ) = O ( n ⋅ log 2 n )
Akra-Bazzi Theorem
分治策略对应的递推式,更一般地形如 T ( n ) = ∑ i = 1 k a i ⋅ T ( b i ⋅ n + h i ( n ) ) + O ( g ( n ) ) \begin{aligned}T(n) = \sum_{i = 1}^k a_i \cdot T(b_i \cdot n + h_i(n)) + O(g(n))\end{aligned} T ( n ) = i = 1 ∑ k a i ⋅ T ( b i ⋅ n + h i ( n ) ) + O ( g ( n ) )
其中 0 < a i , 0 < b i < 1 , ∣ h i ( n ) ∣ = O ( n / log 2 n ) 0 < a_i, 0 < b_i < 1, \left\vert h_i(n) \right\vert = O(n / \log^2n) 0 < a i , 0 < b i < 1 , ∣ h i ( n ) ∣ = O ( n / log 2 n )
0 ≤ g ( n ) 0 \le g(n) 0 ≤ g ( n ) d d d ∣ g ′ ( n ) ∣ = O ( n d ) \left\vert g'(n) \right\vert = O(n^d) ∣ g ′ ( n ) ∣ = O ( n d ) 只要取 p p p ∑ i = 1 k a i ⋅ b i p = 1 \begin{aligned}\sum_{i = 1}^k a_i \cdot b_i^p = 1\end{aligned} i = 1 ∑ k a i ⋅ b i p = 1 T ( n ) = Θ ( n p ⋅ ( 1 + ∫ 1 n g ( u ) / u p + 1 d u ) ) T(n) = \Theta(n^p \cdot (1 + \int_1^n g(u) / u^{p + 1}\, {\rm d}u)) T ( n ) = Θ ( n p ⋅ ( 1 + ∫ 1 n g ( u ) / u p + 1 d u ) )
如对于算法 LinearSelect ,有
T ( n ) = 1 ⋅ T ( 3 / 4 ⋅ n ) + 1 ⋅ T ( 1 / 5 ⋅ n ) + O ( n ) = O ( n ) T(n) = 1 \cdot T(3/4 \cdot n) + 1 \cdot T(1/5 \cdot n) + O(n) = O(n) T ( n ) = 1 ⋅ T ( 3 / 4 ⋅ n ) + 1 ⋅ T ( 1 / 5 ⋅ n ) + O ( n ) = O ( n )
总和最大区段
分而治之
A [ l o , h i ) = A [ l o , m i ) ∪ A [ m i , h i ) = P ∪ S \mathcal{A}[lo, hi) = \mathcal{A}[lo, mi) \cup \mathcal{A}[mi, hi) = \mathcal{P} \cup \mathcal{S} A [ l o , h i ) = A [ l o , m i ) ∪ A [ m i , h i ) = P ∪ S 借助递归,求得 P 、 S \mathcal{P}、\mathcal{S} P 、 S
1 2 3 4 5 6 7 8 9 10 11 12 int gs_DC (int A[], int lo, int hi) if (hi - lo < 2 ) return A[lo]; int mi = (lo + hi) / 2 ; int gsL = A[mi - 1 ], sL = 0 , i = mi; while (lo < i--) if (gsL < (sL += A[i])) gsL = sL; int gsR = A[mi], sR = 0 , j = mi - 1 ; while (++j < hi) if (gsR < (sR += A[j])) gsR = sR; return max (gsL + gsR, max (gs_DC (A, lo, mi), gs_DC (A, mi, hi))); }
减而治之
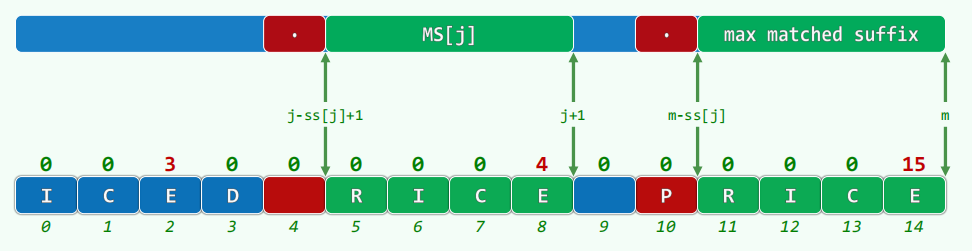
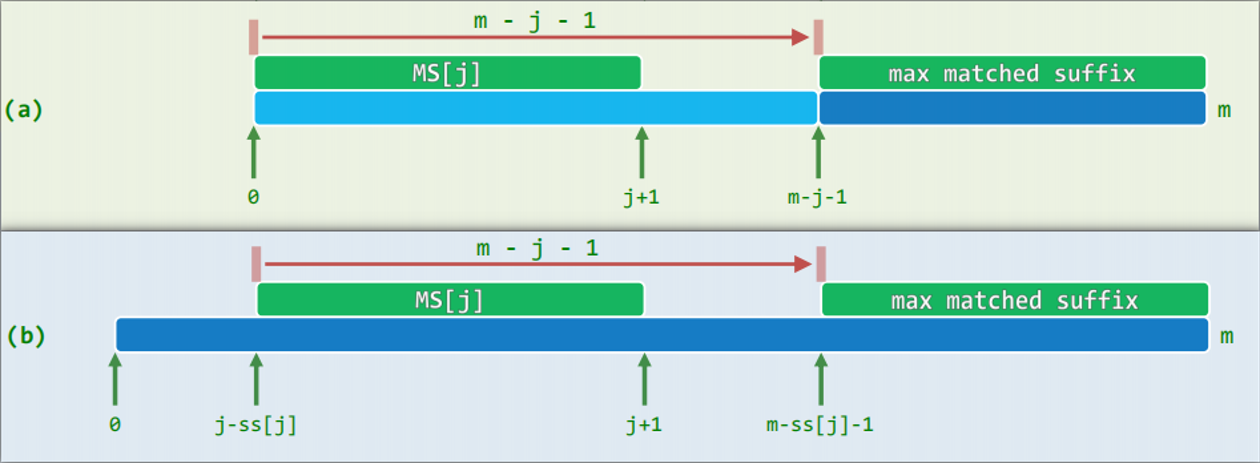
最短的总和非正的后缀 ∼ \sim ∼
若 s u f f i x ( k ) = A [ k , h i ) , k = max { l o ≤ i < h i ∣ s u m [ i , h i ) ≤ 0 } suffix(k) = \mathcal{A}[k, hi), \quad k = \max\{lo \le i < hi | sum[i, hi) \le 0\} s u f f i x ( k ) = A [ k , h i ) , k = max { l o ≤ i < h i ∣ s u m [ i , h i ) ≤ 0 }
则 G S ( l o , h i ) = A [ i , j ) GS(lo, hi) = \mathcal{A}[i, j) G S ( l o , h i ) = A [ i , j ) 后缀 ,要么与之无交
可用反证法证明
1 2 3 4 5 6 7 8 int gs_LS (int A[], int n) int gs = A[0 ], s = 0 , i = n; while (i-- > 0 ) { s += A[i]; if (gs < s) gs = s; if (s <= 0 ) s = 0 ; } }
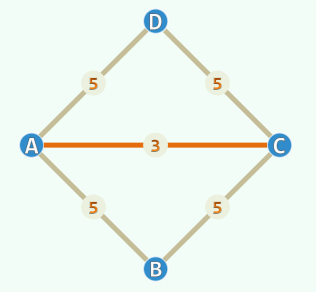
更相减损术
渐进时间复杂度为 O ( log ( a + b ) ) O(\log(a+b)) O ( log ( a + b ) )
1 2 3 4 5 6 7 8 9 10 11 12 13 14 __int64 gcdCN (__int64 a, __int64 b) { int r = 0 ; while (!((a & 1 ) || (b & 1 ))) { a >>= 1 , b >>= 1 , r++; } while (1 ) { while (~(a & 1 )) a >>= 1 ; while (~(b & 1 )) b >>= 1 ; if (a > b) a = a - b; else b = b - a; if (a == 0 ) return b << r; if (b == 0 ) return a << r; } }
动态规划
fib()递归
1 int fib (int n) return (n < 2 ) ? n : fib (n - 1 ) + fib (n - 2 ); }
复杂度:T ( 0 ) = T ( 1 ) = 1 T(0) = T(1) = 1 T ( 0 ) = T ( 1 ) = 1 T ( n ) = T ( n − 1 ) + T ( n − 2 ) , ∀ n > 1 T(n) = T(n - 1) + T(n - 2), \quad \forall n > 1 T ( n ) = T ( n − 1 ) + T ( n − 2 ) , ∀ n > 1
令 S ( n ) = [ T ( n ) + 1 ] / 2 = S ( n − 1 ) + S ( n − 2 ) = f i b ( n + 1 ) S(n) = [T(n) + 1] / 2 = S(n - 1) + S(n - 2) = fib(n + 1) S ( n ) = [ T ( n ) + 1 ] / 2 = S ( n − 1 ) + S ( n − 2 ) = f i b ( n + 1 )
T ( n ) = 2 ⋅ S ( n ) − 1 = 2 ⋅ f i b ( n + 1 ) − 1 = O ( f i b ( n + 1 ) ) = O ( ϕ n ) T(n) = 2 \cdot S(n) - 1 = 2 \cdot fib(n + 1) - 1 = O(fib(n + 1)) = O(\phi ^ n) T ( n ) = 2 ⋅ S ( n ) − 1 = 2 ⋅ f i b ( n + 1 ) − 1 = O ( f i b ( n + 1 ) ) = O ( ϕ n ) 其中 ϕ = ( 1 + 5 ) / 2 \phi = (1 + \sqrt{5}) / 2 ϕ = ( 1 + 5 ) / 2
低效的根源在于,有大量重复的递归实例
记忆化:记住答案,直接“抄袭”(n-1)
Dynamic Programming
1 2 3 4 5 6 7 8 int fib (int n) int f = 1 , g = 0 ; while (n-- > 0 ) { g = g + f; f = g - f; } return g; }
T ( n ) = O ( n ) T(n) = O(n) T ( n ) = O ( n ) O ( 1 ) O(1) O ( 1 )
最长公共子序列
子序列:由序列中若干字符,按原相对次序构成(子串则需要连续)
Longest Common Subsequence:两个序列之间公共子序列中的最长者
分治递归
1 2 3 4 5 6 7 unsigned int lcs (char const *A, int n, const char *B, int m) if (n < 1 || m < 1 ) return 0 ; if (A[n - 1 ] == B[m - 1 ]) return 1 + lcs (A, n - 1 , B, m - 1 ); else return max (lcs (A, n - 1 , B, m), lcs (A, n, B, m)); }
LCS 的每一个解,对应于(0,0)与(n,m)之间的一条单调通路;反之亦然
最好情况 O ( n + m ) O(n + m) O ( n + m )
最坏情况,就是 LCS(A[0], B[0]) 的重复次数,可达 ( n + m n ) \binom{n + m}{n} ( n n + m )
当 n = m n = m n = m Ω ( 2 n ) \Omega(2^n) Ω ( 2 n ) O ( 4 n ) O(4^n) O ( 4 n )
记忆化(或 DP)则只需 O ( n m ) O(nm) O ( n m )
向量
抽象数据类型
数据结构都可看作是由若干数据项组成的集合,同时对数据项定义一组标准的操作。
抽象数据类型(Abstract Data Type,ADT)
将数据结构的外部特性与其内部实现相分离,提供一致且标准的对外接口,隐藏内部的实现细节
数据结构(Data Structure)
从数组到向量
数组
元素各由编号唯一指代,并可直接访问
若每个元素占用空间为 s s s A [ i ] A[i] A [ i ] A + i × s A + i \times s A + i × s
向量
Vector ADT
操作
功能
适用对象
size() / empty()报告元素总数 / 判定是否为空
向量
get(r) / put(r, e)获取秩为 r 的元素 / 用 e 替换秩为 r 元素的数值
向量
insert(r, e) / insert(e)将 e 作为秩为 r 的 / 最后一个元素插入
向量
remove(r) / remove(lo, hi)删除秩为 r/ 区间内的元素
向量
disordered() / sort(lo, hi) / unsort(lo, hi)检测是否整体有序 / 整体排序 / 整体置乱
向量
find(e, lo, hi) / search(e, lo, hi)在指定区间内查找目标 e
向量 / 有序向量
dedup() / uniquify()剔除相等的元素
向量 / 有序向量
traverse( visit() )遍历向量,统一按 visit() 处理所有元素
向量
可扩充的向量
扩容算法
1 2 3 4 5 6 7 8 9 10 11 12 template <typename T> void Vector<T>::copyFrom (T const *A, Rank lo, Rank hi) { _elem = new T[_capacity = (hi - lo) * 2 ]; for (_size = 0 ; lo < hi; _size++, lo++) { _elem[_size] = A[lo]; } } template <typename T> void Vector<T>::expand () { if (_size < _capacity) return ; T* oldElem = _elem; copyFrom (oldElem, 0 , _capacity); delete oldElem; }
分摊分析
容量递增策略
1 _elem = new T[_capacity += INCREMENT];
最坏情况:初始容量 0 的空向量,连续插入 n = m ⋅ I ≫ 2 n = m \cdot I \gg 2 n = m ⋅ I ≫ 2
总体耗时 = 0 + I + ⋯ + ( m − 1 ) ⋅ I = O ( n 2 ) 0 + I + \cdots + (m - 1) \cdot I = O(n^2) 0 + I + ⋯ + ( m − 1 ) ⋅ I = O ( n 2 )
每次插入删除操作分摊成本为 O ( n ) O(n) O ( n )
空间利用率(装填因子):λ = _ s i z e / _ c a p a c i t y ≈ 100 % \lambda = \_size / \_capacity \approx 100\% λ = _ s i z e / _ c a p a c i t y ≈ 1 0 0 %
容量加倍策略
1 _elem = new T[_capacity *= 2 ];
最坏情况:初始容量 1 的满向量,连续插入 n = 2 m ≫ 2 n = 2^m \gg 2 n = 2 m ≫ 2
总体耗时 = 1 + 2 + ⋯ + 2 m − 1 = O ( n ) 1 + 2 + \cdots + 2^{m - 1} = O(n) 1 + 2 + ⋯ + 2 m − 1 = O ( n )
每次(insert/remove)操作分摊成本为 O ( 1 ) O(1) O ( 1 )
λ > 50 % \lambda > 50\% λ > 5 0 %
无序向量
删除
1 2 3 4 5 6 7 8 9 10 11 12 template <typename T> void Vector<T>::shrink () { if (_size << 2 > _capacity) return ; T* oldElem = _elem; _elem = new T[_capacity >>= 1 ]; for (Rank i = 0 ; i < _size; i++) _elem[i] = oldElem[i]; delete oldElem[]; } template <typename T> Rank remove (Rank lo, Rank hi) if (lo == hi) return 0 ; while (hi < _size) _elem[lo++] = _elem[hi++]; _size = lo; shrink (); return hi - lo; }
查找
顺序查找
输入敏感(input-sensitive)
最好 O ( 1 ) O(1) O ( 1 ) O ( n ) O(n) O ( n )
去重
1 2 3 4 5 6 7 8 template <typename T> Rank Vector<T>::dedup () { Rank oldSize = _size; for (Rank i = 1 ; i < _size;) { if (find (_elem[i], 0 , i) == -1 ) i++; else remove (i); } return oldSize - _size; }
有序向量
在有序序列中,任何一对相邻元素必顺序
相邻逆序对的数目,可在一定程度上度量向量的紊乱程度
无序向量经预处理转换为有序向量之后,相关算法多可优化
唯一化
1 2 3 4 5 6 7 8 9 10 template <typename T> Rank Vector<T>::uniquify () { Rank i = 0 , j = 0 ; while (++j < _size) { if (_elem[i] != _elem[j]) { _elem[++i] = _elem[j]; } } _size = ++i; shrink (); return j - i; }
二分查找(版本 A)
减而治之
若轴点 m i mi m i 至多两次 比较
1 2 3 4 5 6 7 8 9 template <typename T> static Rank binSearch (T *S, T const &e, Rank lo, Rank hi) while (lo < hi) { Rank mi = (lo + hi) >> 1 ; if (e < S[mi]) hi = mi; else if (S[mi] < e) lo = mi + 1 ; else return mi; } return -1 ; }
线性“递归”:T ( n ) = T ( n / 2 ) + O ( 1 ) = O ( log n ) T(n) = T(n / 2) + O(1) = O(\log n) T ( n ) = T ( n / 2 ) + O ( 1 ) = O ( log n )
“递归跟踪”:轴点总能取到中点,递归深度 O ( log n ) O(\log n) O ( log n )
关键码的比较次数 ∼ \sim ∼
A S L s u c c = O ( 1.50 ⋅ log n ) ASL_{succ} = O(1.50 \cdot \log n) A S L s u c c = O ( 1 . 5 0 ⋅ log n ) A S L f a i l = O ( 1.50 ⋅ log n ) ASL_{fail} = O(1.50 \cdot \log n) A S L f a i l = O ( 1 . 5 0 ⋅ log n )
Fibonacci 查找
版本 A:转向左、右分支前的关键码比较次数不等,而递归深度却相同
可以通过递归深度的不均衡对转向成本的不均衡做补偿
若 n = f i b ( k ) − 1 n = fib(k) - 1 n = f i b ( k ) − 1 m i = l o + f i b ( k − 1 ) − 1 mi = lo + fib(k - 1) - 1 m i = l o + f i b ( k − 1 ) − 1
前、后子向量长度分别为 f i b ( k − 1 ) − 1 fib(k - 1) - 1 f i b ( k − 1 ) − 1 f i b ( k − 2 ) − 1 fib(k - 2) - 1 f i b ( k − 2 ) − 1
失败查找长度,最大为 k − 1 k - 1 k − 1 k − 2 k - 2 k − 2
成功查找长度,最大为 k − 1 k - 1 k − 1 2 2 2
1 2 3 4 5 6 7 8 9 10 template <typename T> static Rank fibSearch (T *S, T const &e, Rank lo, Rank hi) for (Fib fib (hi - lo); lo < hi;) { while (hi - lo < fib.get ()) fib.prev (); Rank mi = lo + fib.get () - 1 ; if (e < S[mi]) hi = mi; else if (S[mi] < e) lo = mi + 1 ; else return mi; } return -1 ; }
通用策略
在任何区间 [ 0 , n ) [0,n) [ 0 , n ) [ λ ⋅ n ] [\lambda \cdot n] [ λ ⋅ n ] 0 ≤ λ < 1 0 \le \lambda < 1 0 ≤ λ < 1
Fibonacci 查找对应 λ = 1 ϕ = 5 − 1 2 \lambda = \frac{1}{\phi} = \frac{\sqrt{5} - 1}{2} λ = ϕ 1 = 2 5 − 1
这类查找算法的渐近复杂度为 α ( λ ) ⋅ log 2 n = O ( log n ) \alpha(\lambda) \cdot \log_2 n = O(\log n) α ( λ ) ⋅ log 2 n = O ( log n )
递推式:α ( λ ) ⋅ log 2 n = λ ⋅ [ 1 + α ( λ ) ⋅ log 2 ( λ n ) ] + ( 1 − λ ) ⋅ [ 2 + α ( λ ) ⋅ log 2 ( ( 1 − λ ) n ) ] \alpha(\lambda) \cdot \log_2 n = \lambda \cdot [1 + \alpha(\lambda) \cdot \log_2 (\lambda n)] + (1 - \lambda) \cdot [2 + \alpha(\lambda) \cdot \log_2 ((1 - \lambda) n)] α ( λ ) ⋅ log 2 n = λ ⋅ [ 1 + α ( λ ) ⋅ log 2 ( λ n ) ] + ( 1 − λ ) ⋅ [ 2 + α ( λ ) ⋅ log 2 ( ( 1 − λ ) n ) ]
当 λ = 5 − 1 2 \lambda = \frac{\sqrt{5} - 1}{2} λ = 2 5 − 1 α ( λ ) = 1.440420... \alpha(\lambda) = 1.440420... α ( λ ) = 1 . 4 4 0 4 2 0 . . .
二分查找(版本 B)
每次迭代仅做一次关键码比较
e < x → [ l o , m i ) e < x \rightarrow [lo, mi) e < x → [ l o , m i ) x ≤ e → [ m i , h i ) x \le e \rightarrow [mi, hi) x ≤ e → [ m i , h i )
直到 h i − l o = 1 hi - lo = 1 h i − l o = 1
相较于版本 A,最好(坏)情况下更坏(好),整体性能更趋均衡
1 2 3 4 5 6 7 8 template <typename T> static Rank binSearch (T *S, T const &e, Rank lo, Rank hi) while (hi - lo > 1 ) { Rank mi = (lo + hi) >> 1 ; if (e < S[mi]) hi = mi; else lo = mi; } return e == S[lo] ? lo : -1 ; }
返回值改进
约定总是返回 m = s e a r c h ( e ) = M − 1 m = search(e) = M - 1 m = s e a r c h ( e ) = M − 1
− ∞ ≤ m = max { k ∣ [ k ] ≤ e } -\infty \le m = \max\{k | [k] \le e\} − ∞ ≤ m = max { k ∣ [ k ] ≤ e } min { k ∣ e < [ k ] } = M ≤ + ∞ \min\{k | e < [k]\} = M \le +\infty min { k ∣ e < [ k ] } = M ≤ + ∞
直接改进版本 B
return e < S[lo] ? lo - 1 : lo;
二分查找(版本 C)
1 2 3 4 5 6 7 8 9 template <typename T> static Rank binSearch (T *S, T const &e, Rank lo, Rank hi) while (lo < hi) { Rank mi = (lo + hi) >> 1 ; if (e < S[mi]) hi = mi; else lo = mi + 1 ; } return lo - 1 ; }
在算法执行过程中的任意时刻
[ l o − 1 ] [lo - 1] [ l o − 1 ] e e e [ h i ] [hi] [ h i ] e e e
算法终止时,[ l o − 1 ] = [ h i − 1 ] [lo - 1] = [hi - 1] [ l o − 1 ] = [ h i − 1 ] e e e
A S L s u c c = A S L f a i l = O ( 1.00 ⋅ log n ) ASL_{succ} = ASL_{fail} = O(1.00 \cdot \log n) A S L s u c c = A S L f a i l = O ( 1 . 0 0 ⋅ log n )
插值查找
大数定律:越长的序列,元素的分布越有规律
因此,通过猜测轴点 m i mi m i
m i ≈ l o + ( h i − l o ) ⋅ e − A [ l o ] A [ h i ] − A [ l o ] mi \approx lo + (hi - lo) \cdot \frac{e - A[lo]}{A[hi] - A[lo]} m i ≈ l o + ( h i − l o ) ⋅ A [ h i ] − A [ l o ] e − A [ l o ]
最坏情况:h i − l o = O ( n ) hi - lo = O(n) h i − l o = O ( n ) 1 , 1 , … , 2 , 1 0 10 1, 1, \dots, 2, 10^{10} 1 , 1 , … , 2 , 1 0 1 0
平均:每经过一次比较,待查找区间宽度由 n n n n \sqrt{n} n
n → n 1 / 2 1 → n 1 / 2 2 → ⋯ 2 n \rightarrow n^{1/2^1} \rightarrow n^{1/2^2} \rightarrow \cdots 2 n → n 1 / 2 1 → n 1 / 2 2 → ⋯ 2 O ( log log n ) O(\log \log n) O ( log log n )
每经过一次比较,查找区间宽度的数值 n n n log n \log n log n
插值查找 = 在字长意义上的折半查找
二分查找 = 在字长意义上的顺序查找
实际可行的方法:算法接力
先插值查找,迅速缩小查找范围
再改为二分查找,进一步缩小
最后顺序查找
起泡排序
扫描交换,依次比较每一对相邻元素;如有必要,交换之。直至某趟扫描后,确认相邻元素均以顺序。
经过 k k k k k k n − k n - k n − k
至多 n n n
1 2 3 4 5 6 7 8 9 10 template <typename T> void Vector<T>::bubbleSort (Rank lo, Rank hi) { for (Rank last; lo < hi; hi = last) { for (Rank i = (last = lo) + 1 ; i < hi; ) { if (_elem[i - 1 ] > _elem[i]) { swap (_elem[i - 1 ], _elem[i]); last = i; } } } }
时间效率:最好 O ( n ) O(n) O ( n ) O ( n 2 ) O(n^2) O ( n 2 )
在起泡排序中,唯有相邻元素才可交换,故是稳定的
排序算法的稳定性:相等的元素在输入、输出序列中的相对次序,是否保持不变?
比较树
基于比较式算法(Comparison-Based Algorithm,CBA)可以被转换为一个树形结构。该树形结构具有以下性质:
每一内部节点各对应于一次比对操作
内部节点的左、右分支,分别对应与在两种比对结果下的执行方向
叶节点(或根到叶节点的路径)对应于算法某次执行的完整过程及输出
反过来,算法的每一运行过程都对应于从根到某一叶节点的路径
设 C T ( A ) CT(A) C T ( A ) A A A
那么算法 A A A h ( C T ( A ) ) h(CT(A)) h ( C T ( A ) )
算法 A A A Ω ( h ( C T ( A ) ) ) \Omega(h(CT(A))) Ω ( h ( C T ( A ) ) )
若某一问题的输出结果不少于 N N N
比较树叶节点不可能少于 N N N log 2 N \log_2 N log 2 N
由此任一 CBA 式排序算法对应的比较树高度应为
h ≥ ⌈ log 3 ( n ! ) ⌉ = ⌈ log 3 ( e ) ⋅ ln ( n ! ) ⌉ = Ω ( n log n ) h \ge \left \lceil \log_3(n!) \right \rceil = \left \lceil \log_3(e) \cdot \ln(n!) \right \rceil = \Omega(n \log n) h ≥ ⌈ log 3 ( n ! ) ⌉ = ⌈ log 3 ( e ) ⋅ ln ( n ! ) ⌉ = Ω ( n log n ) 最坏情况下 CBA 式排序算法至少需要 Ω ( n log n ) \Omega(n \log n) Ω ( n log n ) n n n
归并排序
1 2 3 4 5 6 7 template <typename T> void Vector<T>::mergeSort (Rank lo, Rank hi) { if (hi - lo < 2 ) return ; Rank mi = (lo + hi) >> 1 ; mergeSort (lo, mi); mergeSort (mi, hi); merge (lo, mi, hi); }
二路归并
1 2 3 4 5 6 7 8 9 10 11 12 template <typename T> void Vector<T>::merge (Rank lo, Rank mi, Rank hi) { Rank i = 0 ; T* A = _elem + lo; Rank j = 0 , lb = mi - lo; T* B = new T[lb]; for (Rank i = 0 ; i < lb; i++) B[i] = A[i]; Rank k = 0 , lc = hi - mi; T* C = _elem + mi; while ((j < lb) && (k < lc)) A[i++] = (B[j] <= C[k]) ? B[j++] : C[k++]; while (j < lb) A[i++] = B[j++]; delete [] B; }
复杂度
二路归并每次累计迭代步数 ≤ l b + l c = n \le lb + lc = n ≤ l b + l c = n O ( n ) O(n) O ( n )
总体 T ( n ) = 2 ⋅ T ( n / 2 ) + O ( n ) = O ( n log n ) T(n) = 2 \cdot T(n / 2) + O(n) = O(n \log n) T ( n ) = 2 ⋅ T ( n / 2 ) + O ( n ) = O ( n log n )
优点
最坏情况下最优 O ( n log n ) O(n\log n) O ( n log n )
不需随机读写,完全顺序访问
实现恰当,可保证稳定
适用于外部排序,易于并行化
缺点
非就地 即使输入已完全(或接近)有序,仍需 Ω ( n log n ) \Omega(n \log n) Ω ( n log n )
位图
典型应用
小集合+大数据
筛法
1 2 3 4 5 6 7 8 9 10 11 void Erathsthenes (Rank n, char *file) Bitmap B (n) ; B.set (0 ), B.set (1 ); for (Rank i = 2 ; i < n; i++) { if (!B.test (i)) { for (Rank j = 2 * i; j < n; j+= i) { B.set (j); } } } B.dump (file); }
内循环每趟迭代 O ( n / i ) O(n / i) O ( n / i ) n ln n \frac{n}{\ln n} l n n n
n 2 + n 3 + n 5 + ⋯ < n 2 + n 3 + n 4 + ⋯ + n n / ln n = O ( n ⋅ ( ln ( n / ln n ) − 1 ) ) = O ( n ⋅ log n ) \begin{aligned}&\frac{n}{2} + \frac{n}{3} + \frac{n}{5} + \cdots \\ < \quad &\frac{n}{2} + \frac{n}{3} + \frac{n}{4} + \cdots + \frac{n}{n / \ln n} \\ = \quad &O(n \cdot (\ln(n / \ln n) - 1)) = O(n \cdot \log n) \end{aligned} < = 2 n + 3 n + 5 n + ⋯ 2 n + 3 n + 4 n + ⋯ + n / ln n n O ( n ⋅ ( ln ( n / ln n ) − 1 ) ) = O ( n ⋅ log n )
常系数优化:内循环的起点可以改为 i * i ,外循环的终止条件可以改为 i * i < n
快速初始化
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 Rank F[m]; Rank T[m], top = 0 ; bool Bitmap::test (Rank k) return (F[k] != -1 ) && (F[k] < top) && (k == T[F[k]]); } void Bitmap::reset () 0 ; } void Bitmap::set (Rank k) if (!test (k)) { T[top] = k; F[k] = top++; } } void Bitmap::clear (Rank k) if (test (k) && (--top)) { F[T[top]] = F[k]; T[F[k]] = T[top]; } }
列表
循位置访问
列表(list)是采用 动态 储存策略的典型结构
元素称为节点,通过引用或者指针彼此联接
在 逻辑上 构成一个线性序列,各元素的物理地址将不再决定逻辑次序
动态操作可以在局部完成,复杂度有望控制在 O ( 1 ) O(1) O ( 1 )
循位置访问:利用节点之间的相互引用,找到特定的节点
如果按逻辑次序进行连续访问,单次也是 O ( 1 ) O(1) O ( 1 )
call-by-position
接口与实现
ListNode
操作接口
功能
pred() / succ()当前节点的前驱/后继节点的位置
data()当前节点所存数据对象
insertPred() / insertSucc()插入前驱/后继节点,返回新节点位置
List ADT
操作接口
功能
适用对象
size() / empty()报告节点总数 / 判定是否为空
列表
first() / last()返回首 / 末节点的位置
列表
insertFirst() / insertLast()将 e 当作首 / 末节点插入
列表
insert(p, e) / insert(e, p)将 e 当作节点 p 的 直接 后继、前驱插入
列表
remove(p)删除节点 p
列表
sort(p, n) / sort()区间 / 整体排序
列表
find(e, n, p) / search(e, n, p)在指定区间内查找目标 e
列表 / 有序列表
dedup() / uniquify()剔除相等的节点
列表 / 有序列表
traverse(visit())遍历列表,统一按 visit() 处理所有节点
列表
1 2 3 4 5 6 7 8 9 ListNodePosi<T> head, tail; template <typename T> void List<T>::init () { head = new ListNode<T>; tail = new ListNode<T>; head->succ = tail; head->pred = null; tail->pred = head; tail->succ = null; _size = 0 ; }
1 2 3 4 5 template <typename T> T& List<T>::operator [] (Rank r) const { ListNodePosi<T> p = first (); while (r-- > 0 ) p = p->succ; return p->data; }
有序列表
唯一化
1 2 3 4 5 6 7 8 9 template <typename T> Rank List<T>::uniquify () { if (_size < 2 ) return 0 ; Rank oldSize = _size; ListNodePost<T> p = first (), q; while (tail != (q = p->succ ())) { if (p->data != q->data) p = q; else remove (q); } }
查找
1 2 3 4 5 6 template <typename T> ListNodePost<T> List<T>::search (T const &e, Rank n, ListNodePosi<T> p) const { do { p = p->pred; n--; } while ((n != -1 ) && (e < p->data)); return p; }
最好 O ( 1 ) O(1) O ( 1 ) O ( n ) O(n) O ( n ) O ( n ) O(n) O ( n )
不能借助有序性提高查找效率,因为无法高效实现秩的随机访问
选择排序
起泡排序扫描交换的实质无非是
通过比较找到当前的最大元素 M M M
其中 O ( n ) O(n) O ( n )
在经 O ( n ) O(n) O ( n ) M M M
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 template <typename T> ListNodePosi<T> List<T>::selectMax (ListNodePosi<T> p, rank n) { ListNodePosi<T> max = p; for (ListNodePosi<T> cur = p; n > 1 ; n--) { if (!((cur = cur->succ)->data < max->data)) max = cur; } return max; } template <typename T> void List<T>::selectionSort (ListNodePosi<T> p, Rank n) { ListNodePosi<T> h = p->pred; ListNodePosi<T> t = p; for (Rank i = 0 ; i < n; i++) t = t->succ; while (n > 1 ) { insert (remove (selectMax (h->succ, n)), t); t = t->pred; n--; } }
采用 平移法 ,可保证稳定性;每一组相等的元素,都保持输入时的相对次序
总体时间复杂度为 Θ ( n 2 ) \Theta(n^2) Θ ( n 2 )
循环节
任何一个序列 A [ 0 , n ) \mathcal{A}[0,n) A [ 0 , n )
元素 A [ k ] \mathcal{A}[k] A [ k ] S [ 0 , n ) \mathcal{S}[0, n) S [ 0 , n ) r ( A [ k ] ) = r ( k ) ∈ [ 0 , n ) r(\mathcal{A}[k]) = r(k) \in [0, n) r ( A [ k ] ) = r ( k ) ∈ [ 0 , n )
k , r ( k ) , r ( r ( k ) ) , … , r ( … ( r ( r ( k ) ) ) … ) = k k, r(k), r(r(k)), \dots, r(\dots (r(r(k))) \dots) = k k , r ( k ) , r ( r ( k ) ) , … , r ( … ( r ( r ( k ) ) ) … ) = k r 0 ( k ) , r 1 ( k ) , r 2 ( k ) , … , r ( d ) ( k ) = k r^0(k), r^1(k), r^2(k), \dots, r^{(d)}(k) = k r 0 ( k ) , r 1 ( k ) , r 2 ( k ) , … , r ( d ) ( k ) = k
任意循环节长度 d ≤ n d \le n d ≤ n
对于 交换法 选择排序
每迭代一步,M M M
M M M
多余的交换:M M M
最初有 c c c c − 1 c-1 c − 1
最大值为 n n n Θ ( log n ) \Theta(\log n) Θ ( log n )
插入排序
始终将序列视为两部分
前缀 S [ 0 , r ) S[0, r) S [ 0 , r )
后缀 U [ r , n ) U[r, n) U [ r , n )
反复地,针对 e = A [ r ] e = A[r] e = A [ r ] S S S e e e r r r
1 2 3 4 5 6 template <typename T> void List<T>::insertionSort (ListNodePosi<T> p, Rank n) { for (Rank r = 0 ; r < n; r++) { insert (search (p->data, r, p), p->data); p = p->succ (); remove (p->pred); } }
前缀总是保持有序且稳定
最好 O ( n ) O(n) O ( n ) O ( n 2 ) O(n^2) O ( n 2 ) O ( n 2 ) O(n^2) O ( n 2 )
可 在线 执行
归并排序
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 template <typename T> ListNodePosi<T> List<T>::merge (ListNodePosi<T> p, Rank n, List<T> &L, ListNodePosi<T> q, Rank m) { ListNodePosi<T> pp = p->pred; while (m > 0 && p != q) { if (n > 0 && p->data <= q->data) { p = p->succ; n--; } else { insert (L.remove ((q = q->succ)->pred), p); m--; } } return pp->succ; } template <typename T> void List<T>::mergeSort (ListNodePosi<T> &p, Rank n) { if (n < 2 ) return ; ListNodePosi<T> q = p; Rank m = n >> 1 ; for (Rank i = 0 ; i < m; i++) q = q->succ; mergeSort (p, m); mergeSort (q, n - m); p = merge (p, m, *this , q, n - m); }
逆序对
I ( j ) = ∥ { 0 ≤ i < j ∣ A [ i ] > A [ j ] } ∥ \mathcal{I}(j) = \lVert \{ 0 \le i < j \, | \, A[i] > A[j]\} \rVert I ( j ) = ∥ { 0 ≤ i < j ∣ A [ i ] > A [ j ] } ∥ 逆序对总数 I = ∑ I ( j ) ≤ ( n 2 ) = O ( n 2 ) \mathcal{I} = \sum \mathcal{I}(j) \le \binom{n}{2} = O(n^2) I = ∑ I ( j ) ≤ ( 2 n ) = O ( n 2 )
BubbleSort
在序列中交换一对紧邻的逆序元素,逆序对总数恰好减一
对于起泡排序而言,交换操作的次数恰等于输入序列所含逆序对总数
InsertionSort
每次迭代查找插入位置,恰好需要做 I ( r ) \mathcal{I}(r) I ( r )
若序列共含 I \mathcal{I} I
关键码比较次数为 O ( I ) O(\mathcal{I}) O ( I )
运行时间为 O ( n + I ) O(n + \mathcal{I}) O ( n + I )
若任意逆序对距离不超过 k k k O ( k ⋅ n ) O(k \cdot n) O ( k ⋅ n )
计数
朴素算法需要 Ω ( n 2 ) \Omega(n^2) Ω ( n 2 ) O ( n log n ) O(n \log n) O ( n log n )
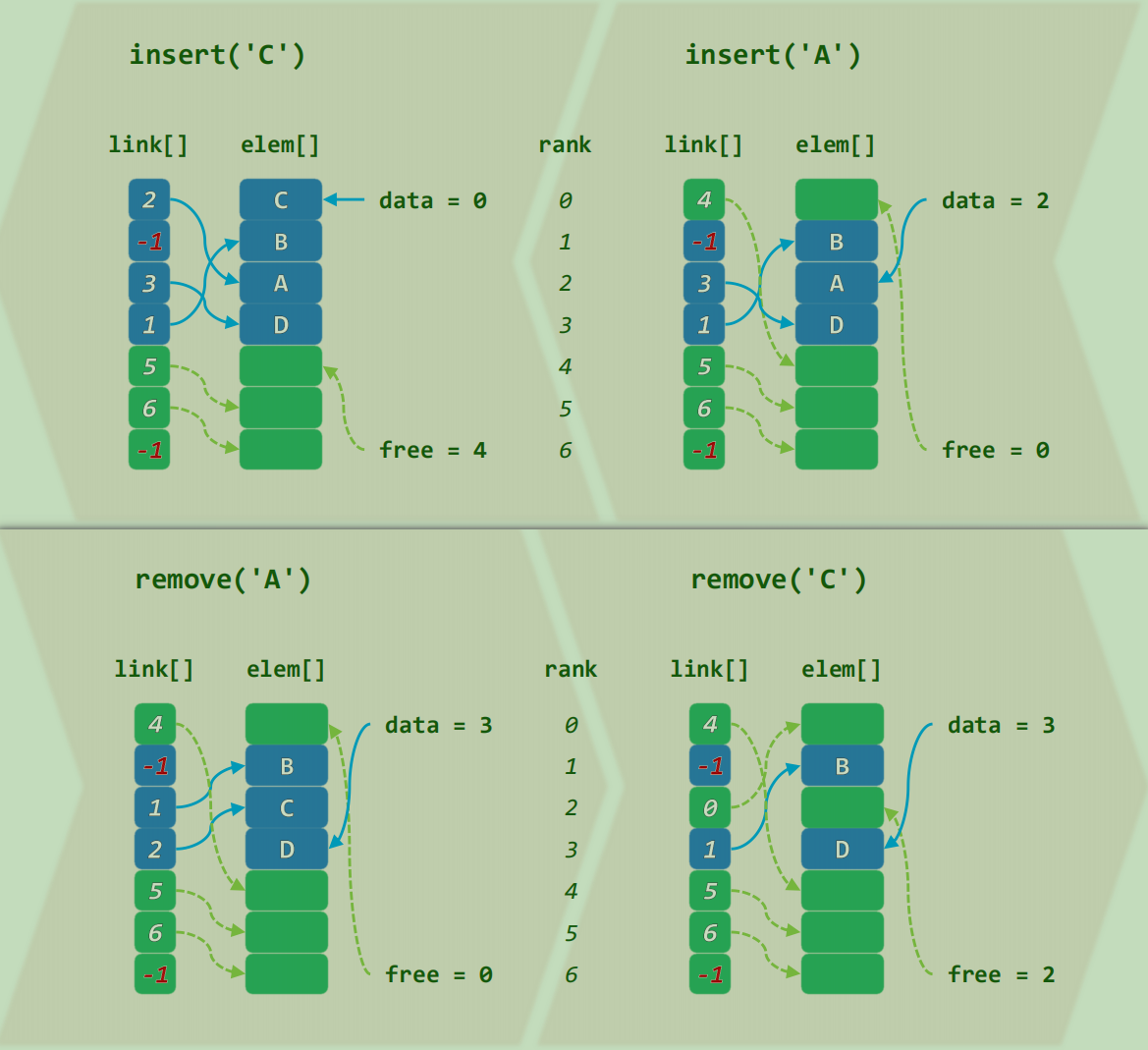
游标实现
在一块连续的静态内存(数组)中,模拟出链表的动态链接特性
所需结构如下:
一个结构数组或两个独立数组
elem[] :存放数据元素的数组link[] :存放“指针”的数组,称之为游标
link[i] 的值是 elem[i] 的后继元素所在的 elem[] 下标
两个 逻辑 上互补的链表
data :存放当前存在的所有数据free :存放所有当前空闲、可被分配的数组槽位
两个“头指针”(头游标)
dataHead :存储 data 链表的第一个元素所在的数组下标freeHead :存储 free 链表的第一个可用槽位所在的数组下标
空指针标记
需要一个特殊值来表示链表的末尾(相当于 NULL),约定使用 -1 来表示
1 2 3 4 5 6 7 8 const int N = 1000 ;int elem[N], link[N], data, free;void init () free = 0 , data = -1 ; for (int i = 0 ; i < N - 1 ; i++) link[i] = i + 1 ; link[N - 1 ] = -1 ; }
核心操作
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 int allocNode () if (free == -1 ) return -1 ; int nw = free; free = link[free]; return nw; } void freeNode (int index) link[index] = free; free = index; } int insert (int value) int newIndex = allocNode (); if (newIndex == -1 ) return -1 ; elem[newIndex] = value; link[newIndex] = data; data = newIndex; return newIndex; } int find (int value) int r; for (r = data; r != -1 ; r = link[r]) { if (elem[r] == value) return r; } return -1 ; } bool remove (int pos) int idx = link[pos]; if (idx == -1 ) return false ; link[pos] = link[idx]; freeNode (idx); return true ; }
栈和队列
栈
接口与实现
栈(stack)是受限的序列
只能在栈顶(top)插入和删除,栈底为盲端
后进先出(LIFO)
可直接基于向量或者列表派生
1 2 3 4 5 6 template <typename T> class Stack : public Vector<T> {public : void push (T const &e) insert (e); } T pop () { return remove (size () - 1 ); } T &top () { return (*this )[size () - 1 ]; } };
以向量首端为栈底,末端为栈顶,由此实现的栈接口,均只需 O ( 1 ) O(1) O ( 1 )
调用栈
递归算法所需的空间主要取决于递归深度,而非递归实例总数
消除递归
隐式地维护调用栈,需要花费额外的空间、时间;为此可
显示地维护调用栈
将递归算法改写为迭代版本(改写尾递归)
时间复杂度有常系数改进,空间复杂度 或有 渐近改进
进制转换
短除法:对进制 λ \lambda λ λ \lambda λ
位数 m + 1 = ⌊ log λ n ⌋ + 1 m + 1 = \left \lfloor \log_\lambda n \right \rfloor + 1 m + 1 = ⌊ log λ n ⌋ + 1
1 2 3 4 5 6 7 8 9 10 11 12 void convert (Stack<char > &S, unsigned long long n, int base) char digit[] = "0123456789ABCDEF" ; while (n > 0 ) { S.push (digit[n % base]); n /= base; } } main () { Stack<char > S; (n > 0 ) ? convert (S, n, base) : S.push ('0' ); while (!S.empty ()) S.pop (); }
括号匹配
平凡:无括号的表达式是匹配的
为有效简化问题,需发现和借助 必要性
消去一对紧邻的左右括号,不影响全局的匹配判断
顺序扫描表达式,用栈记录已扫描的部分
反复迭代:凡遇 ( ,则进栈;凡遇 ) ,则出栈
1 2 3 4 5 6 7 8 9 bool paren (const char exp[], Rank lo, Rank hi) Stack<char > S; for (Rank i = lo; i < hi; i++) { if (exp[i] != '(' ) S.push (exp[i]); else if (!S.empty ()) S.pop (); else return false ; } return S.empty (); }
中缀表达式求值
给定语法正确的算数表达式 S \mathcal{S} S
减而治之:优先级高的局部表达式执行计算,并被代以其数值,运算符减少,直至得到最终结果
但仅根据表达式的前缀,不足以确定各运算符的计算次序
为处理某一前缀,必须提前 预读并分析更长的前缀
需借助某种支持延迟缓冲的机制
求值算法 = 栈 + 线性扫描
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 const char pri[N_OPTR][N_OPTR] = { }; double evaluate (char *S, char *RPN) Stack<double > opnd; Stack<char > optr; optr.push ('\0' ); while (!optr.empty ()) { if (isdigit (*S)) { readNumber (S, opnd); } else { switch (priority (optr.top (), *S)) { case '<' : optr.push (*S); S++; break ; case '>' : char op = optr.pop (); if (op != '!' ) { opnd.push (calcu (op, opnd.pop ())); } else { double opnd2 = opnd.pop (), opnd1 = opnd.pop (); opnd.push (calcu (opnd1, op, opnd2)); } break ; case '~' : optr.pop (); S++; break ; default : exit (-1 ); } } } return opnd.pop (); }
逆波兰表达式
定义和求值
Reverse Polish Notation,在由运算符(operator)和操作数(operand)组成的表达式中,不使用括号,即可表示带优先级的运算关系
相较于日常使用的中缀式(infix),RPN 亦称作后缀式(postfix)
作为补偿,须额外引入一个起分隔作用的原字符(如空格)
栈式求值(不会检查式子合法性)
引入栈 S \mathcal{S} S
逐个处理下一元素 x
若 x 是操作数,则将其压入 S
否则(运算符无序缓冲)
从 S 中弹出 x 所需数目的操作数
进行运算,结果压入 S
返回栈顶结果
转换
手工转换
为每一个运算添加括号
以运算符替换右括号,并清除对应左括号
自动转换
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 double evaluate (char *S, char *RPN) while (!optr.empty ()) { if (isdigit (*S)) { readNumber (S, pond); append (RPN, opnd.top ()); } else { switch (priority (optr.top (), *S)) { case '>' : char op = optr.pop (); append (RPN, op); } } } }
栈混洗
考察栈 A = ⟨ a 1 , a 2 , … , a n ] , B = S = ∅ \mathcal{A} = \left \langle a_1, a_2, \dots, a_n \right.], \quad \mathcal{B} = \mathcal{S} = \varnothing A = ⟨ a 1 , a 2 , … , a n ] , B = S = ∅
只允许
将 A 的顶元素弹出并压入 S
将 S 的顶元素弹出并压入 B
经一系列上述操作,A 中元素全部转入 B 中
B = [ a k 1 , a k 2 , … , a k n ⟩ \mathcal{B} = [\left. a_{k_1}, a_{k_2}, \dots, a_{k_n} \right \rangle B = [ a k 1 , a k 2 , … , a k n ⟩
计数
同一输入序列,可有多种栈混洗
对于长度为 n n n S P ( n ) ≤ n ! SP(n) \le n! S P ( n ) ≤ n !
S P ( 1 ) = 1 SP(1) = 1 S P ( 1 ) = 1
考查 S 再度变空(A 首元素从 S 中弹出)的时刻,无非 n n n
S P ( n ) = ∑ k = 1 n S P ( k − 1 ) ⋅ S P ( n − k ) = Catalan ( n ) = ( 2 n ) ! ( n + 1 ) ! ⋅ n ! \begin{aligned} SP(n) &= \sum_{k = 1}^n SP(k - 1) \cdot SP(n - k) \\ &=\text{Catalan}(n) = \frac{(2n)!}{(n + 1)! \cdot n!} \end{aligned} S P ( n ) = k = 1 ∑ n S P ( k − 1 ) ⋅ S P ( n − k ) = Catalan ( n ) = ( n + 1 ) ! ⋅ n ! ( 2 n ) !
甄别
输入序列 ⟨ 1 , 2 , 3 , … , n ] \left \langle 1, 2, 3, \dots, n \right.] ⟨ 1 , 2 , 3 , … , n ] [ p 1 , p 2 , p 3 , … , p n ⟩ [\left. p_1, p_2, p_3, \dots, p_n \right \rangle [ p 1 , p 2 , p 3 , … , p n ⟩
禁形:对任何 1 ≤ i < j < k ≤ n , [ … , k , … , i , … , j , … ⟩ 1 \le i < j < k \le n, \quad [\left. \dots, k, \dots, i, \dots, j, \dots \right \rangle 1 ≤ i < j < k ≤ n , [ … , k , … , i , … , j , … ⟩
不存在 “312(915)” 模式的序列 ⟺ \iff ⟺ O ( n 3 ) O(n^3) O ( n 3 )
进一步,[ p 1 , p 2 , … , p n ⟩ [\left. p_1, p_2, \dots, p_n \right \rangle [ p 1 , p 2 , … , p n ⟩ ⟨ 1 , 2 , … , n ] \left \langle 1, 2, \dots, n \right.] ⟨ 1 , 2 , … , n ]
对于任意 i < j i < j i < j [ … , j + 1 , … , i , … , j , … ⟩ [\left. \dots, j + 1, \dots, i, \dots, j, \dots \right \rangle [ … , j + 1 , … , i , … , j , … ⟩
O ( n ) O(n) O ( n )
逐个检视各目标元素
若在(或能腾挪至)S 顶部,则继续
否则(在 S 中,却非栈顶,无法洗出)失败
总结
Catalan ( n ) \text{Catalan}(n) Catalan ( n )
n n n n n n push 和 n n n pop 对应的合法操作序列数)n n n n n n n n n n + 1 n + 1 n + 1 叶节点 (n n n 中序遍历是 1 ∼ n 1\sim n 1 ∼ n
n + 1 n + 1 n + 1 n n n n + 2 n + 2 n + 2 圆上 2 n 2n 2 n n n n
n × n n \times n n × n
队列
接口与实现
队列(queue)也是受限的序列
只能在队尾插入(查询)
只能在队头删除(查询)
先进先出(FIFO)
1 2 3 4 5 6 template <typename T> class Queue : public List<T> {public : void enqueue (T const &e) insertLast (e); } T dequeue () { return remove (first ()); } T &front () { return first ()->data; } }
如此实现的队列接口,均只需 O ( 1 ) O(1) O ( 1 )
队列应用
直方图内最大矩形
对每个位置 r r r
s ( r ) = max { k ∣ 0 ≤ k ≤ r ∩ H [ k − 1 ] < H [ r ] } s(r) = \max\{k \, | \, 0 \le k \le r \cap H[k - 1] < H[r]\} s ( r ) = max { k ∣ 0 ≤ k ≤ r ∩ H [ k − 1 ] < H [ r ] } t ( r ) = min { k ∣ r < k ≤ n ∩ H [ r ] > H [ k ] } t(r) = \min\{k \, | \, r < k \le n \cap H[r] > H[k]\} t ( r ) = min { k ∣ r < k ≤ n ∩ H [ r ] > H [ k ] } a n s w e r = max { H [ r ] ⋅ ( t ( r ) − s ( r ) ) } answer = \max\{H[r] \cdot (t(r) - s(r))\} a n s w e r = max { H [ r ] ⋅ ( t ( r ) − s ( r ) ) } 可以 O ( n 2 ) O(n^2) O ( n 2 ) 单调栈 通过两次线性扫描得出
若要优化至一次扫描,则可使用单调栈 S 维持高度 H 的单调递增
若栈空或 H[t] < H[S.top()] ,则直接压栈
否则,不断弹栈,直到将当前高度压栈后可保持单调性;同时在这过程中不断计算更新面积最大值
1 2 3 4 5 6 7 8 9 Stack<Rank> SR; unsigned long long maxRect = 0 ; for (Rank t = 0 ; t <= n; t++) { while (!SR.empty () && (t == n || H[SR.top ()] > H[t])) { Rank r = SR.pop (), s = SR.empty () ? 0 : SR.top () + 1 ; maxRect = max (maxRect, (t - s) * H[r]); } if (t < n) SR.push (t); } return maxRect;
Steap
Steap = Stack + Heap = push + pop +getMax = S + PP 中每个元素,都是 S 中对应前缀的最大者
1 2 3 Steap::getMax () { return P.top (); } Steap::pop () { P.pop (); return S.pop (); } Steap::push () { P.push (max (e, P.top ())); S.push (e); }
Queap
Queap = Queue + Heap = enqueue + dequeue + getMax = Q + P
1 2 3 4 5 6 7 Queap::dequeue () { P.dequeue (); return Q.dequeue (); } Queap::enqueue () { Q.enqueue (e); P.enqueue (e); for (auto x = P.rear (); x && (e >= x->key); x = x->pred) { x->key = e; } }
双栈当队
1 2 3 4 5 6 7 8 def Q .enqueue(e): R.push(e) def Q .dequeue(): if F.empty(): while !R.empty(): F.push(R.pop()) return F.pop()
均摊复杂度为 O ( 1 ) / O ( 1 ) O(1) / O(1) O ( 1 ) / O ( 1 )
二叉树
概述
动机
层次结构的表示
兼具 Vector 和 List 的优点,兼顾高效的查找、插入、删除
不再是简单的线性结构,
有根树
树是极小连通图、极大无环图 T = ( V ; E ) \mathcal{T} = (V; \, E) T = ( V ; E )
节点数 n = ∣ V ∣ n = \left\vert V \right\vert n = ∣ V ∣ e = ∣ E ∣ e = \left\vert E \right\vert e = ∣ E ∣
删边不连通,加边必成环
指定任一节点 r ∈ V r \in V r ∈ V T \mathcal{T} T
相对于 T \mathcal{T} T T i \mathcal{T}_i T i r i r_i r i T i = subtree ( r i ) \mathcal{T}_i = \text{subtree}(r_i) T i = subtree ( r i )
有序树
r i r_i r i r r r r i r_i r i d = degree ( r ) d = \text{degree}(r) d = degree ( r ) r r r
e = ∑ v ∈ V degree ( v ) = n − 1 = Θ ( n ) e = \sum_{v \in V} \text{degree}(v) = n - 1 = \Theta(n) e = ∑ v ∈ V degree ( v ) = n − 1 = Θ ( n )
若指定 T i \mathcal{T}_i T i T \mathcal{T} T i i i r i r_i r i r r r i i i T \mathcal{T} T
深度
路径长度即为所含边数
∣ π ∣ = ∣ { ( v 0 , v 1 ) , ( v 1 , v 2 ) , … , ( v k − 1 , v k ) } ∣ = k \left\vert \pi \right\vert = \left\vert \{(v_0, v_1), (v_1, v_2), \dots, (v_{k - 1}, v_k)\} \right\vert = k ∣ π ∣ = ∣ { ( v 0 , v 1 ) , ( v 1 , v 2 ) , … , ( v k − 1 , v k ) } ∣ = k 环路:v 0 = v k v_0 = v_k v 0 = v k
任一节点 v v v
path ( v , r ) = path ( v ) \text{path}(v, r) = \text{path}(v) path ( v , r ) = path ( v ) 该路径上节点,均为 v v v
v v v depth ( v ) = ∣ path ( v ) ∣ \text{depth}(v) = \left\vert \text{path}(v) \right\vert depth ( v ) = ∣ path ( v ) ∣ 没有后代的节点称作叶子节点
所有叶子 深度 中的最大者称作(子)树的高度
height ( v ) = height ( subtree ( v ) ) \text{height}(v) = \text{height}(\text{subtree}(v)) height ( v ) = height ( subtree ( v ) ) 空树高度为-1
depth ( v ) + height ( v ) ≤ height ( T ) \text{depth}(v) + \text{height}(v) \le \text{height}(\mathcal{T}) depth ( v ) + height ( v ) ≤ height ( T )
二叉树
节点度数不超过 2,孩子可以左、右区分(隐含有序)
有根且有序的多叉树,可以转化表示为二叉树
长子 ∼ \sim ∼
兄弟 ∼ \sim ∼
基数
设度数为 0、1 和 2 的节点,各有 n 0 n_0 n 0 n 1 n_1 n 1 n 2 n_2 n 2
边数 e = n − 1 = n 1 + 2 n 2 e = n - 1 = n_1 + 2 n_2 e = n − 1 = n 1 + 2 n 2
叶节点数 n 0 = n 2 + 1 n_0 = n_2 + 1 n 0 = n 2 + 1
真二叉树
所有节点度数均为偶数(n 1 = 0 n_1 = 0 n 1 = 0
所有二叉树均可通过引入 2 n 0 + n 1 2 n_0 + n_1 2 n 0 + n 1 外部节点 转换为二叉树
转换之后,全树复杂度 Θ ( n ) \Theta(n) Θ ( n )
节点总数为奇数,树的最大高度为 n − 1 2 \frac{n - 1}{2} 2 n − 1
满树
深度为 k k k 2 k 2^k 2 k
n n n h h h h + 1 ≤ n ≤ 2 h + 1 − 1 h + 1 \le n \le 2^{h + 1} - 1 h + 1 ≤ n ≤ 2 h + 1 − 1
n = h + 1 n = h + 1 n = h + 1 n = 2 h + 1 − 1 n = 2^{h + 1} - 1 n = 2 h + 1 − 1
模版类和实现
1 2 3 4 5 6 7 8 9 10 11 template <typename T> using BinNodePosi = BinNode<T>*;template <typename T> struct BinNode { BinNodePosi<T> parent, lc, rc; T data; Rank height, npl; RBColor color; Rank size () ; Rank updateHeight () ; void updateHeightAbove () BinNodePosi<T> insertLc (T const &) ; BinNodePosi<T> insertRc (T const &) ; BinNodePosi<T> succ () ; }
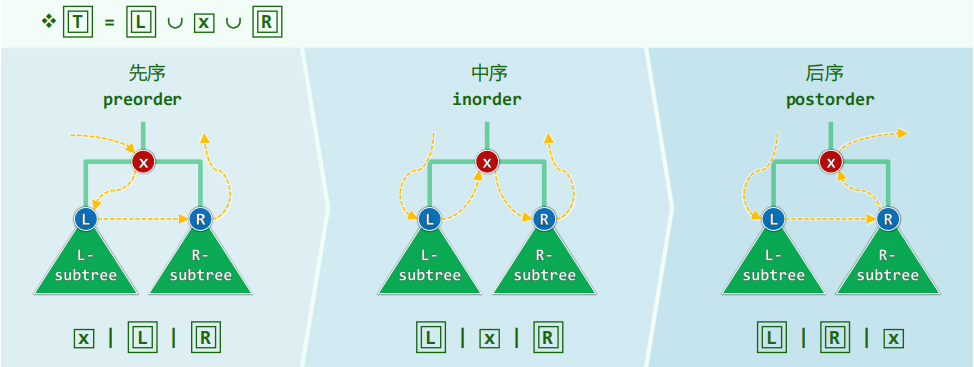
先序遍历
遍历:按照某种次序访问树中各节点,每个节点被访问恰好一次
递归实现
1 2 3 4 5 6 template <typename T, typename VST> void traverse (BinNodePosi<T> x, VST &visit) if (!x) return ; visit (x->data); traverse (x->lc, visit); traverse (x->rc, visit); }
迭代实现
藤 = 起始于根的 左侧 通路 = 长子通路
沿着藤,整个遍历过程可被分为
各右子树的遍历彼此独立,自成一个子任务
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 template <typename T, typename VST> static void visitAlongVine (BinNodePosi<T> x, VST &visit, Stack<BinNodePosi<T>> &S) while (x) { visit (x->data); if (x->rc) S.push (x->rc); x = x->lc; } } template <typename T, typename VST> void travPre_I2 (BinNodePosi<T> x, VST &visit) Stack<BinNodePosi> S; while (true ) { visitAlongVine (x, visit, S); if (S.empty ()) break ; x = S.pop (); } }
中序遍历
整个树结构向下投影即为中序遍历序列
递归实现
1 2 3 4 5 6 7 template <typename T, typename VST>void traverse (BinNodePosi<T> x, VST &visit) if (!x) return ; traverse (x->lc, visit); visit (x->data); traverse (x->rc, visit); }
迭代实现
沿藤分解,遍历过程可 自底向上 分解为 d + 1 d+1 d + 1
各右子树的遍历彼此独立,自成一个 子任务
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 template <typename T> static void goAloneVine (BinNodePosi<T> x, Stack<BinNodePosi<T>> &S) while (x) { S.push (x); x = x->lc; } } template <typename T, typename VST> void travIn_I1 (BinNodePosi<T> x, V &visit) Stack<BinNodePosi<T>> S; while (true ) { goAloneVine (x, S); if (S.empty ()) break ; x = S.pop (); visit (x->data); x = x->rc; } }
直接后继
简明遍历
1 for (BinNodePosi<T> t = first (); t; t = t->succ ()) { }
若节点有右孩子,则直接后继为最靠左的右后代
否则,其直接后继为最低的左祖先
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 template <typename T> BinNodePosi<T> BinNode<T>::succ () { BinNodePosi<T> s = this ; if (rc) { s = rc; while (HasLChild (s)) s = s->lc; } else { while (isRChild (s)) s = s->parent; s = s->parent; } return s; } template <typename T, typename VST> void travIn_I4 (BinNodePosi<T> x, VST &visit) while (true ) { if (HasLChild (x)) x = x->lc; else { visit (x->data); while (!HasRChild (x)) { if (!(x = x->succ ())) return ; visit (x->data); } x = x->rc; } } }
实际上,在由 n n n u u u v v v ∣ u v ∣ \left\vert uv \right\vert ∣ u v ∣ { v 0 , v 1 , v 2 , … , v n − 1 } \{v_0,v_1,v_2,\dots,v_{n-1}\} { v 0 , v 1 , v 2 , … , v n − 1 } ∣ v 0 v 1 ∣ + ∣ v 1 v 2 ∣ + ⋯ + ∣ v n − 2 v n − 1 ∣ + ∣ v n − 1 v 0 ∣ = 2 ( n − 1 ) \left\vert v_0v_1 \right\vert + \left\vert v_1v_2 \right\vert + \dots + \left\vert v_{n-2}v_{n-1} \right\vert + \left\vert v_{n-1}v_0 \right\vert = 2(n-1) ∣ v 0 v 1 ∣ + ∣ v 1 v 2 ∣ + ⋯ + ∣ v n − 2 v n − 1 ∣ + ∣ v n − 1 v 0 ∣ = 2 ( n − 1 )
后序遍历
递归实现
1 2 3 4 5 6 7 template <typename T, typename VST>void traverse (BinNodePosi<T> x, VST &visit) if (!x) return ; traverse (x->lc, visit); traverse (x->rc, visit); visit (x->data); }
迭代实现
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 template <typename T> static void gotoLeftmostLeaf (Stack<BinNodePosi<T>> &S) while (BinNodePosi<T> x = S.top ()) { if (HasLChild (x)) { if (HasRChild (x)) { S.push (x->rc); } S.push (x->lc); } else { S.push (x->rc); } } S.pop (); } template <typename T, typename VST>void travPost_I (BinNodePosi<T> x, V &visit) Stack<BinNodePosi<T>> S; if (x) S.push (x); while (!S.empty ()) { if (S.top () != x->parent) { gotoLeftmostLeaf (S); } x = S.pop (); visit (x->data); } }
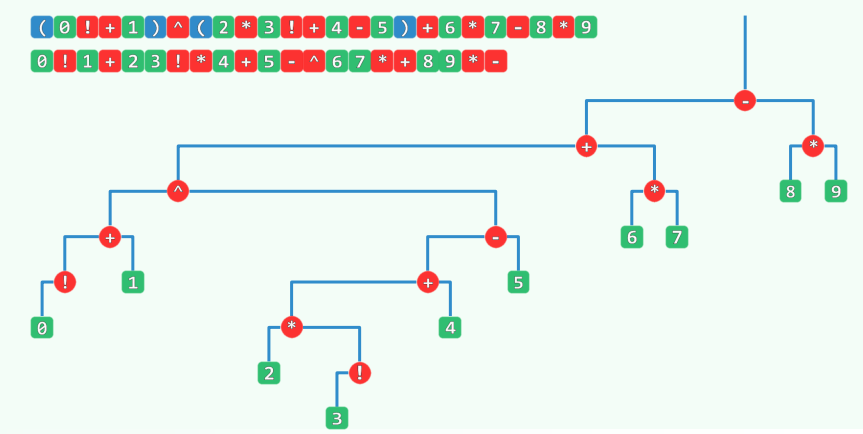
表达式树
Expression Tree ∼ \sim ∼ ∼ \sim ∼
由 RPN 转表达式树:
从左至右依次遍历
操作数则形成叶子节点压入栈中
操作符则弹出相应数目节点组成子树,再入栈
层次遍历
实现
1 2 3 4 5 6 7 8 9 10 11 template <typename T, typename VST>void BinNode<T>::travLevel (VST &visit) { Queue<BinNodePosi<T>> Q; Q.enqueue (this ); while (!Q.empty ()) { BinNodePosi<T> x = Q.dequeue (); visit (x->data); if (HasLChild (x)) Q.enqueue (x->lc); if (HasRChild (x)) Q.enqueue (x->rc); } }
完全二叉树
重构
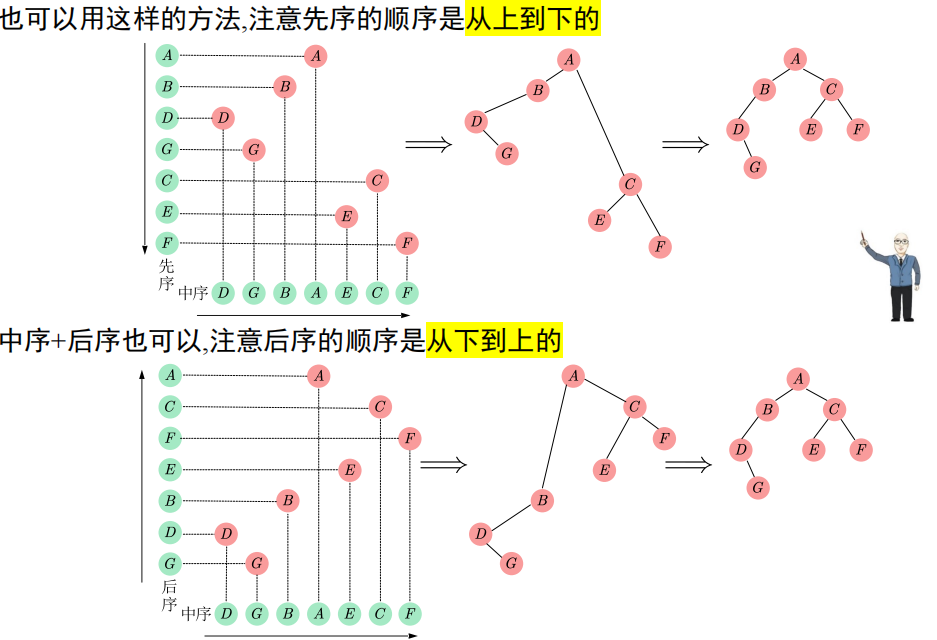
由 [ 先序 | 后序 | 层次 ] + 中序可确定一棵树的形态
原理在于前者可以确定根,后者可以由根将左右子树区分开
由 [ 先序 + 后序 ] 则无法确定形态
在无法确定树的几何结构的情况下
[ 后序 + 层次 ] 可以得出唯一的先序遍历序列
[ 先序 + 后序 ] 可以得出唯一的层次遍历序列
增强序列
将每个 NULL 也看作真实节点,并在遍历时输出约定的元字符(如“^”)
可归纳证明,在增强的先序、后序遍历序列中
任一子树依然对应一个子序列,并且
其中 NULL 节点恰好比非 NULL 节点多一(n 0 = n 2 + 1 n_0 = n_2 + 1 n 0 = n 2 + 1
可以对增强序列分而治之,重构出原树
但是增强的中序遍历序列无法重构
增强的层次遍历序列可以重构
Huffman 编码树
二进制编码
组成数据文件的字符来自字符集 Σ \Sigma Σ
字符被赋予 互异 的二进制串
PFC 编码
Prefix-Free Code,为了避免某字符的编码恰是另一字符编码的前缀二叉编码树
Σ \Sigma Σ x x x v ( x ) v(x) v ( x ) x 的编码串由根到 v ( x ) v(x) v ( x )
如此自然保证了 Prefix-Free
效率度量:平均编码长度
ald ( T ) = ∑ x ∈ Σ depth ( v ( x ) ) / ∣ Σ ∣ \text{ald}(T) = \sum_{x \in \Sigma} \text{depth}(v(x)) / \left\vert \Sigma \right\vert ald ( T ) = ∑ x ∈ Σ depth ( v ( x ) ) / ∣ Σ ∣
最优编码树
叶子只能出现在倒数两层以内——否则,通过节点交换一定可以更优
带权编码
各字符的期望频率已知,则
文件长度 ∝ \propto ∝ wald ( T ) = ∑ x r p s ( x ) × w ( x ) \text{wald}(T) = \sum_x rps(x) \times w(x) wald ( T ) = ∑ x r p s ( x ) × w ( x )
此时完全树 未必就是 最优编码树
最优带权编码树
仍具有 双子 性
频率高/低的字符,应尽可能放在高/低处
通过适当交换,可以缩短 wald ( T ) \text{wald}(T) wald ( T )
出现频率最低的字符 x x x y y y
否则,进行适当交换后,wald \text{wald} wald
Huffman 编码树
贪心策略
1 2 3 4 5 6 7 为每个字符创建一棵单节点的树, 组成森林F 按照出现频率对所有树排序 while F中的树不止一棵 取出频率最小的两棵树: T1, T2 将他们合并成一棵新树T, 并令 lc(T) = T1, rc(T) = T2 w(root(T)) = w(root(T1)) + w(root(T2))
实现与改进
使用向量或列表,O ( n 2 ) O(n^2) O ( n 2 )
使用优先级队列,O ( n log n ) O(n\log n) O ( n log n )
使用预排序 + 栈 + 队列,O ( n log n ) O(n\log n) O ( n log n )
所有字符按频率非升序入栈(也可使用队列)
维护另一队列有序,O ( n ) O(n) O ( n )
过程类似于二路归并
二叉搜索树
概述
向量、列表并不能兼顾静态查找与动态修改
综合二者优点,各数据项依所持关键码而彼此区分
call-by-key关键码之间必须支持比较(大小)和比对(相等)(全序)
二叉搜索树
顺序性:任一节点均不小/大于其左/右后代
BST 的中序遍历序列,必然 单调 非降
算法及实现
查找
从根节点出发,逐步地缩小查找范围,直到
发现目标(成功),或抵达空树(失败)
整个过程仿效有序向量的二分查找
1 2 3 4 5 6 7 8 9 10 template <typename T> BinNodePosi<T>& BST::search (const T &e) if (!_root || e == _root->data) { _hot = NULL ; return _root; } for (_hot = _root; ; ) { BinNodePosi<T> &v = (e < _hot->data) ? _hot->lc : _hot->rc; if (!v || e == v->data) return v; _hot = v; } }
可将失败的情况假想为,将该空节点转换为一个数值为 e e e
插入
1 2 3 4 5 6 7 template <typename T> BinNodePosi<T> BST::<T>insert (const T &e) { BinNodePosi<T> &x = search (e); if (x) return x; x = new BinNode <T>(e, _hot); _size++; x->updateHeightAbove (); return x; }
时间主要消耗于 search(e) 和 updateHeightAbove(x)
删除
1 2 3 4 5 6 7 template <typename T> bool BST<T>::remove (const T &e) { BinNodePosi<T> &x = search (e); if (!x) return false ; removeAt (x, _hot); _size--; _hot->updateHeightAbove (); return true ; }
单分支
若 x x x 直接替换 为另一棵子树
双分支
若 x x x
则找到 x x x w = x.succ()
交换 x x x w w w w w w 必无左孩子 )
1 2 3 4 5 6 7 8 9 10 11 12 13 14 template <typename T> static BinNodePosi<T> removeAt (BinNodePosi<T> &x, BinNodePosi<T> hot) BinNodePosi<T> w = x, succ = NULL ; if (!HasLChild (x)) succ = x = x->rc; else if (!HasRChild (x)) succ = x = x->lc; else { w = w->succ (); swap (x->data, w->data); BinNodePosi<T> u = w->parent; (u == x ? u->rc : u->lc) = succ = w->rc; } hot = x->parent; if (succ) succ->parent = hot; delete w; return succ; }
平衡
BST 的主要接口 search() 、insert() 、remove() 在最坏情况下,均线性正比于树高 O ( h ) O(h) O ( h )
若不能有效地控制树高,最(较)坏情况下 BST 将会退化为列表
随机生成分析
n n n { e 1 , e 2 , … , e n } \{e_1, e_2, \dots, e_n\} { e 1 , e 2 , … , e n } σ = { e i 1 , e i 2 , … , e i n } \sigma = \{e_{i1}, e_{i2}, \dots, e_{in}\} σ = { e i 1 , e i 2 , … , e i n } 若各排列出现的概率均等,则 BST 平均高度为 Θ ( log n ) \Theta(\log n) Θ ( log n )
计入 remove() ,则可通过随机使用 succ() 和 pred() ,避免逐渐倾侧
随机组成分析
n n n 拓扑联接 由 n n n S ( n ) S(n) S ( n )
S ( n ) = ∑ k = 1 n S ( k − 1 ) ⋅ S ( n − k ) = catalan ( n ) = ( 2 n ) ! n ! ⋅ ( n + 1 ) ! S(n) = \sum_{k = 1}^n S(k - 1) \cdot S(n - k) = \text{catalan}(n) = \frac{(2n)!}{n! \cdot (n + 1)!} S ( n ) = ∑ k = 1 n S ( k − 1 ) ⋅ S ( n − k ) = catalan ( n ) = n ! ⋅ ( n + 1 ) ! ( 2 n ) !
假定所有 BST 等概率出现,则平均高度为 Θ ( n ) \Theta(\sqrt{n}) Θ ( n )
在 Huffman 编码等应用中,二叉树的确是逐渐 拼合 而成的
理想平衡
由 n n n ⌊ log 2 n ⌋ \left\lfloor \log_2 n \right\rfloor ⌊ log 2 n ⌋
达到这一下界时,为理想平衡
大致相当于完全二叉树甚至满树
维护成本过高
高度渐进地不超过 O ( log n ) O(\log n) O ( log n )
渐进平衡的 BST,简称为平衡二叉搜索树 BBST
等价变换
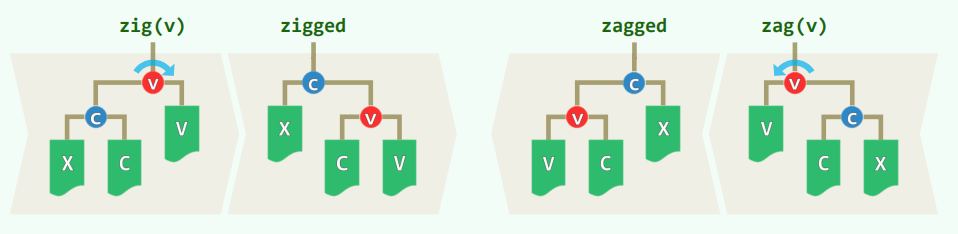
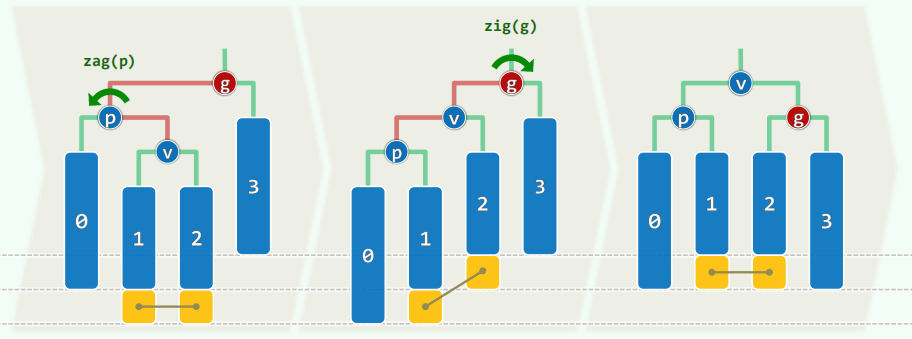
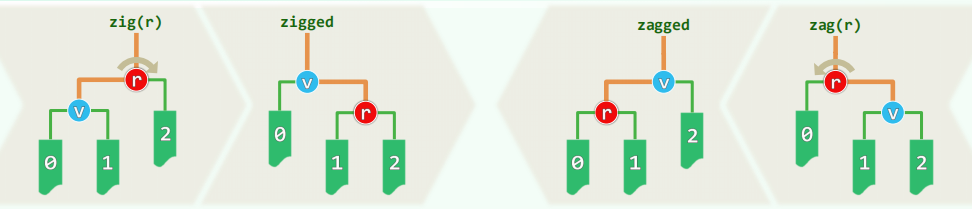
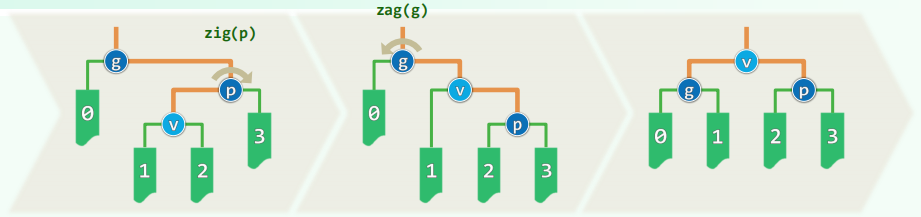
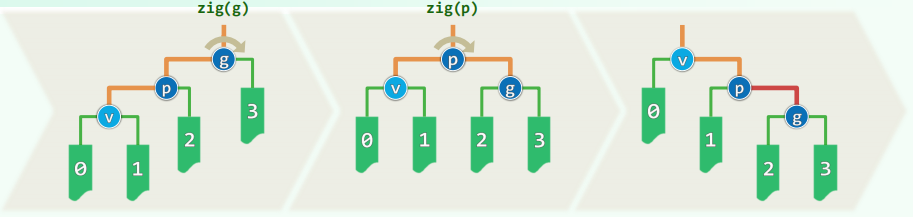
旋转调整
刚刚失衡的 BBST,必可迅速转换为一棵等价的 BBST
为此只需 O ( log n ) O(\log n) O ( log n ) O ( 1 ) O(1) O ( 1 )
实际上,经过不超过 O ( n ) O(n) O ( n )
规模 为 n n n n − 1 n - 1 n − 1
考虑 BST 的最左侧通路,从该通路的末端节点 L d L_d L d
若 L d L_d L d zag 调整,否则上升至父节点继续
任一节点需要通过旋转归入最左侧通路,当且仅当它最初不在该通路上
AVL 树
渐进平衡
平衡因子 b a l F a c ( v ) = h e i g h t ( l c ( v ) ) − h e i g h t ( r c ( v ) ) balFac(v) = height(lc(v)) - height(rc(v)) b a l F a c ( v ) = h e i g h t ( l c ( v ) ) − h e i g h t ( r c ( v ) )
∀ v ∈ AVL , ∣ b a l F a c ( v ) ∣ ≤ 1 \forall v \in \text{AVL}, \, \left\vert balFac(v) \right\vert \le 1 ∀ v ∈ AVL , ∣ b a l F a c ( v ) ∣ ≤ 1
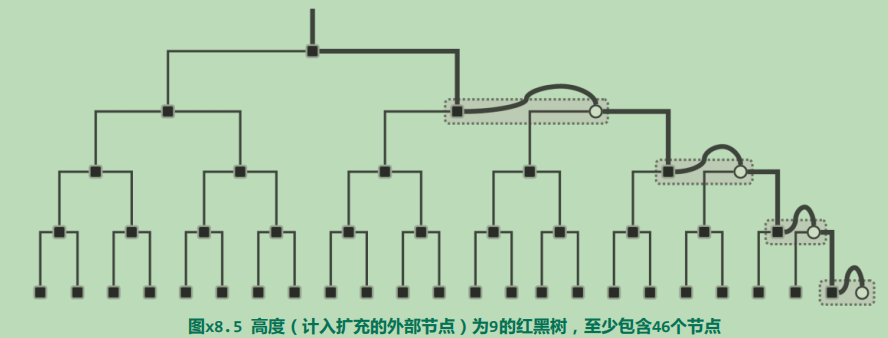
高度为 h h h S ( h ) = f i b ( h + 3 ) − 1 S(h) = fib(h + 3) - 1 S ( h ) = f i b ( h + 3 ) − 1
S ( h ) = 1 + S ( h − 1 ) + S ( h − 2 ) S(h) = 1 + S(h - 1) + S(h - 2) S ( h ) = 1 + S ( h − 1 ) + S ( h − 2 ) 反过来,由 n n n O ( log n ) O(\log n) O ( log n )
高度为 h h h ⌈ h / 2 ⌉ \lceil h / 2 \rceil ⌈ h / 2 ⌉
失衡和恢复
插入
黄色节点 恰好 存在其一
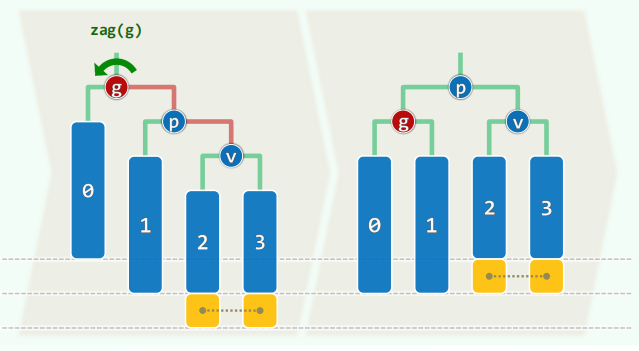
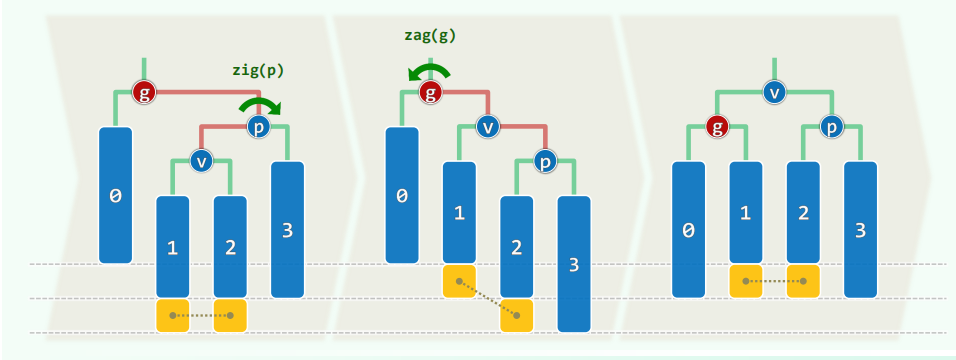
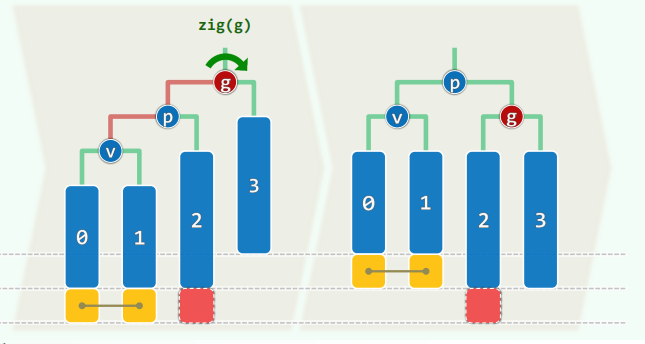
可能有多个失衡节点,最低者 g g g x x x
g g g 高度复原 更高祖先也必平衡,全树复衡
逐层上溯,即可找到 g g g
p = tallerChild(g) ,v = tallerChild(p)
p、v 方向一致则单旋,否则双旋,至多 O ( 1 ) O(1) O ( 1 )
1 2 3 4 5 6 7 8 9 10 11 template <typename T> BinNodePosi<T> AVL<T>::insert (const T &e) { BinNodePosi<T> &x = search (e); if (x) return x; BinNodePosi<T> xx = x = new BinNode <T>(e, _hot); _size++; for (BinNodePosi<T> g = _hot; g; g->updateHeight (), g = g->parent) { if (!AvlBalanced (g)) { rotateAt (tallerChild (tallerChild (g))); break ; } } }
删除
黄色节点至少存在其一,红色节点可有可无
瞬时至多一个失衡节点 g g g x x x _hot
复衡后子树高度 未必复原
故失衡可能持续向上传播,最多需要做 O ( log n ) O(\log n) O ( log n )
逐层上溯,找到 g g g
p = tallerChild(g) ,v = tallerChild(p)
p、v 方向一致则单旋,否则双旋
1 2 3 4 5 6 7 8 9 10 11 template <typename T> bool AVL<T>::remove (const T &e) { BinNodePosi<T> &x = search (e); if (!x) return false ; removeAt (x, _hot); _size--; for (BinNodePosi<T> g = _hot; g; g->updateHeight (), g = g->parent) { if (!AvlBalanced (g)) { rotateAt (tallerChild (tallerChild (g))); } } return true ; }
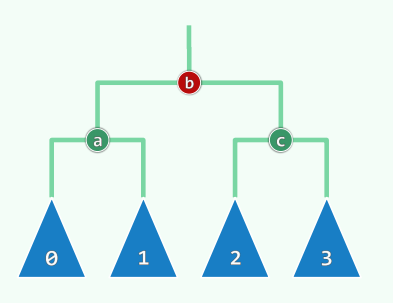
(3+4)-重构
设 g g g 最长分支 考察祖孙三代 g ∼ p ∼ v g \sim p \sim v g ∼ p ∼ v
按中序遍历次序,重命名为 a < b < c a < b < c a < b < c
四棵子树(可能空),按中序遍历次序,重命名为 T 0 < T 1 < T 2 < T 3 T_0 < T_1 < T_2 < T_3 T 0 < T 1 < T 2 < T 3
将原先以 g g g b b b
等价代换,保持中序遍历次序 $ T_0 < a < T_1 < b < T_2 < c < T_3$
1 2 3 4 5 6 7 8 9 10 11 12 template <typename T> BinNodePosi<T> BST<T>::connect34 ( BinNodePosi<T> a, BinNodePosi<T> b, BinNodePosi<T> c, BinNodePosi<T> T0, BinNodePosi<T> T1, BinNodePosi<T> T2, BinNodePosi<T> T3 ) { a->lc = T0; if (T0) T0->parent = a; a->rc = T1; if (T1) T1->parent = a; c->lc = T2; if (T2) T2->parent = c; c->rc = T3; if (T3) T3->parent = c; b->lc = a, a->parent = b; b->rc = c, c->parent = b; a->updateHeight (); c->updateHeight (); b->updateHeight (); return b; }
1 2 3 4 5 6 7 8 9 10 11 12 template <typename T> BinNodePosi<T> BST<T>::rotateAt (BinNodePosi<T> v) { BinNodePosi<T> p = v->parent; int TurnV = IsRChild (v); BinNodePosi<T> g = p->parent; int TurnP = IsRChild (p); BinNodePosi<T> r = (TurnP == TurnV) ? p : v; (FromParentTo (g) = r)->parent = g->parent; switch ((TurnP << 1 ) | TurnV) { case 0b00 : return connect34 (v, p, g, v->lc, v->rc, p->rc, g->rc); case 0b01 : return connect34 (p, v, g, p->lc, v->lc, v->rc, g->rc); case 0b10 : return connect34 (g, v, p, g->lc, v->lc, v->rc, p->rc); default : return connect34 (g, p, v, g->lc, p->lc, v->lc, v->rc); } }
总结
优点
无论查找、插入或删除,最坏情况下的复杂度均为 O ( log n ) O(\log n) O ( log n )
缺点
借助高度或平衡因子,为此需改造元素结构,或额外封装
实测复杂度与理论值尚有差距
插入/删除后的旋转,成本不菲
删除操作后,最多旋转 Ω ( log n ) \Omega(\log n) Ω ( log n ) 0.21 次)
单次动态调整后,全树 拓扑结构的变化量 可能高达 Ω ( log n ) \Omega(\log n) Ω ( log n )
高级搜索树
伸展树
局部性:刚被访问过的数据,极有可能很快地再次被访问
BST 的局部性
时间:刚被访问过的节点,极有可能很快地再次被访问
空间:下一将要访问的节点,极有可能就在刚被访问过节点的附近
对于 AVL 的连续 m ≫ n m \gg n m ≫ n O ( m log n ) O(m\log n) O ( m log n )
利用局部性加速:BST 的节点一旦被访问,随即调整到树根
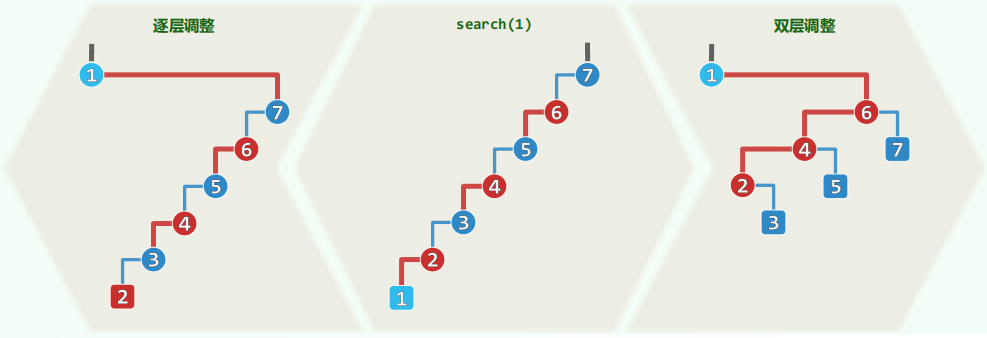
单层伸展
节点 v 一旦被访问,随即被推送至根
旋转次数呈周期性的算术级数(周期访问所有节点)
每一周期结构会复原,累计 Ω ( n 2 ) \Omega(n^2) Ω ( n 2 ) Ω ( n ) \Omega(n) Ω ( n )
双层伸展
反复考察祖孙三代
g = parent(p), p = parent(v), v根据他们的相对位置,经 两次旋转 ,使 v 上升两层,成为子树根
zig-zag 操作本身就是平衡的,效果很好对于 zig-zig,先 p 后 g 只会拉长和移动访问路径,无法改善树的整体结构;而先 g 后 p 则能够“折叠”和“打散”访问路径
zig 和 zag 不同组合,共计 4 种
节点访问之后,对应路径的长度随即 折半
最坏情况显然 O ( n ) O(n) O ( n )
分摊仅需 O ( log n ) O(\log n) O ( log n )
算法实现
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 template <typename T> BinNodeposi<T> Splay<T>::splay (BinNodePosi<T> v) { BinNodePosi<T> p, q; while ((p = v->parent) && (g = p->parent)) { BinNodePosi<T> gg = g->parent; switch ((IsLChild (p) << 1 ) | IsLChild (v)) { case 0b00 : ; case 0b01 : ; case 0b10 : ; default : ; } if (!gg) v->parent = NULL ; else (g == gg->lc) ? gg->attachLc (v) : gg->attachRc (v); g->updateHeight (); p->updateHeight (); v->updateHeight (); } if (p = v->parent) { if (IsLChild (v)) { p->attachLc (v->rc); v->attachRc (p); } else { p->attachRc (v->lc); v->attachLc (p); } p->updateHeight (); v->updateHeight (); } v->parent = NULL ; return v; }
查找
与常规 BST::search() 不同,很可能会改变树的拓扑结构, 不再属于静态操作
1 2 3 4 5 template <typename T> BinNodePosi<T>& Splay<T>::search (const T &e) { BinNodePosi<T> p = BST<T>::search (e); _root = p ? splay (p) : _hot ? splay (_hot) : NULL ; return _root; }
插入
Splay::search() 查找失败后,_hot 即为根
1 2 3 4 5 6 7 8 9 10 11 12 13 template <typename T> BinNodePosi<T> Splay<T>::insert (T const &e) { if (_root) { _size = 1 ; return _root = new BinNode <T>(e); } BinNodePosi<T> t = search (e); if (t->data == e) return t; if (t->data < e) { _root = new BinNode <T>(e, NULL , t, t->rc); t->rc = NULL ; } else { _root = new BinNode <T>(e, NULL , t->lc, t); t->lc = NULL ; } _size++; t->updateHeightAbove (); return _root; }
删除
同插入,search() 后可直接在树根附近摘除节点
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 template <typename T> bool Splay<T>::remove (T const &e) { if (!root || e != search (e)->data) return false ; BinNodePosi<T> L = _root->lc, R = _root->rc; delete _root; if (!R) { if (L) L->parent = NULL ; _root = L; } else { _root = R; R->parent = NULL ; search (e); _root->attachLc (L); } _size--; if (_root) _root->updateHeight (); return true ; }
总结
无需记录高度或平衡因子,编程实现简单,分摊复杂度 O ( log n ) O(\log n) O ( log n )
局部性强,缓存命中率极高时(k ≪ n ≪ m k \ll n \ll m k ≪ n ≪ m k k k
效率甚至可以更高,自适应的 O ( log k ) O(\log k) O ( log k )
任何 连续 的 m m m O ( m log k + n log n ) O(m\log k + n\log n) O ( m log k + n log n )
若 反复地顺序 访问任意子集,分摊成本仅为常数
不能杜绝 单次最坏 情况,不适用于对效率敏感的场合
分摊分析
势能
任何一棵伸展树在任何时刻,都可假想地视作具有势能
Φ ( S ) = log ( ∏ v ∈ S s i z e ( v ) ) = ∑ v ∈ S log ( s i z e ( v ) ) = ∑ v ∈ S r a n k ( v ) = ∑ v ∈ S log V \Phi(S) = \log(\prod_{v \in S} size(v)) = \sum_{v \in S} \log(size(v)) = \sum_{v \in S} rank(v) = \sum_{v \in S} \log V Φ ( S ) = log ( ∏ v ∈ S s i z e ( v ) ) = ∑ v ∈ S log ( s i z e ( v ) ) = ∑ v ∈ S r a n k ( v ) = ∑ v ∈ S log V
越平衡/倾侧的树,势能越小/大
单链
Φ ( S ) = log n ! = O ( n log n ) \Phi(S) = \log n! = O(n \log n) Φ ( S ) = log n ! = O ( n log n )
满树
Φ ( S ) = log ∏ d = 0 h ( 2 h − d + 1 − 1 ) 2 d ≤ log ∏ d = 0 k 2 ( h − d + 1 ) ⋅ 2 d = ∑ d = 0 h ( h − d + 1 ) ⋅ 2 d = ( h + 1 ) ⋅ ( 2 h + 1 − 1 ) − [ ( h − 1 ) ⋅ 2 h + 1 + 2 ] = 2 h + 2 − h − 3 = O ( n ) \begin{aligned}\Phi(S) &= \log \prod_{d = 0}^h (2^{h - d + 1} - 1)^{2^d} \le \log \prod_{d = 0}^k 2^{(h - d + 1) \cdot 2^d} \\ &= \sum_{d = 0}^h (h - d + 1) \cdot 2^d = (h + 1) \cdot (2^{h + 1} - 1) - [(h - 1)\cdot 2^{h + 1} + 2] \\ &= 2^{h + 2} - h - 3 = O(n) \end{aligned} Φ ( S ) = log d = 0 ∏ h ( 2 h − d + 1 − 1 ) 2 d ≤ log d = 0 ∏ k 2 ( h − d + 1 ) ⋅ 2 d = d = 0 ∑ h ( h − d + 1 ) ⋅ 2 d = ( h + 1 ) ⋅ ( 2 h + 1 − 1 ) − [ ( h − 1 ) ⋅ 2 h + 1 + 2 ] = 2 h + 2 − h − 3 = O ( n )
总体关系推导
考察对伸展树 S S S m ≫ n m \gg n m ≫ n search() )
记 A ( k ) = T ( k ) + Δ Φ ( k ) A^{(k)} = T^{(k)} + \Delta \Phi^{(k)} A ( k ) = T ( k ) + Δ Φ ( k )
T ( k ) T^{(k)} T ( k ) k k k Δ Φ ( k ) = Φ a f t e r − Φ b e f o r e \Delta \Phi^{(k)} = \Phi_{after} - \Phi_{before} Δ Φ ( k ) = Φ a f t e r − Φ b e f o r e k k k
则有 T = ∑ k = 1 m T ( k ) = ∑ k = 1 m ( A ( k ) − Δ Φ ( k ) ) = A − Δ Φ T = \sum_{k = 1}^m T^{(k)} = \sum_{k = 1}^m (A^{(k)} - \Delta \Phi^{(k)}) = A - \Delta \Phi T = ∑ k = 1 m T ( k ) = ∑ k = 1 m ( A ( k ) − Δ Φ ( k ) ) = A − Δ Φ
其中 ∣ Δ Φ ∣ ≤ O ( n log n ) \left\vert \Delta\Phi \right\vert \le O(n \log n) ∣ Δ Φ ∣ ≤ O ( n log n )
故 T = A ± O ( n log n ) T = A \pm O(n \log n) T = A ± O ( n log n )
T ( k ) T^{(k)} T ( k ) A ( k ) A^{(k)} A ( k ) v v v
A ( k ) = O ( r a n k ( k ) ( v ) − r a n k ( k − 1 ) ( v ) ) = O ( log n ) A^{(k)} = O(rank^{(k)}(v) - rank^{(k - 1)}(v)) = O(\log n) A ( k ) = O ( r a n k ( k ) ( v ) − r a n k ( k − 1 ) ( v ) ) = O ( log n )
伸展操作分析
反向双旋(zig-zag / zag-zig),( log G i + log P i ) / 2 ≤ log ( ( G i + P i ) / 2 ) < log ( V i / 2 ) (\log G_i + \log P_i) / 2\le \log ((G_i + P_i) / 2) < \log (V_i / 2) ( log G i + log P i ) / 2 ≤ log ( ( G i + P i ) / 2 ) < log ( V i / 2 )
A i ( k ) = T i ( k ) + Δ Φ i ( k ) = 2 + Δ r a n k i ( g ) + Δ r a n k i ( p ) + Δ r a n k i ( v ) = 2 + [ r a n k i ( g ) − r a n k i − 1 ( g ) ] + [ r a n k i ( p ) − r a n k i − 1 ( p ) ] + [ r a n k i ( v ) − r a n k i − 1 ( v ) ] < 2 + r a n k i ( g ) + r a n k i ( p ) − 2 ⋅ r a n k i − 1 ( v ) < 2 + 2 ⋅ r a n k i ( v ) − 2 − 2 ⋅ r a n k i − 1 ( v ) = 2 ⋅ ( r a n k i ( v ) − r a n k i − 1 ( v ) ) \begin{aligned} A^{(k)}_i &= T^{(k)}_i + \Delta\Phi^{(k)}_i = 2 + \Delta rank_i(g) + \Delta rank_i(p) + \Delta rank_i(v) \\ &= 2 + [rank_i(g) - \cancel{rank_{i - 1}(g)}] + [rank_i(p) - rank_{i - 1}(p)] + [\cancel{rank_i(v)} - rank_{i - 1}(v)] \\ &< 2 + rank_i(g) + rank_i(p) - 2 \cdot rank_{i - 1}(v) \\ &< 2 + 2 \cdot rank_i(v) - 2 - 2 \cdot rank_{i - 1}(v) \\ &= 2 \cdot(rank_i(v) - rank_{i - 1}(v)) \end{aligned} A i ( k ) = T i ( k ) + Δ Φ i ( k ) = 2 + Δ r a n k i ( g ) + Δ r a n k i ( p ) + Δ r a n k i ( v ) = 2 + [ r a n k i ( g ) − r a n k i − 1 ( g ) ] + [ r a n k i ( p ) − r a n k i − 1 ( p ) ] + [ r a n k i ( v ) − r a n k i − 1 ( v ) ] < 2 + r a n k i ( g ) + r a n k i ( p ) − 2 ⋅ r a n k i − 1 ( v ) < 2 + 2 ⋅ r a n k i ( v ) − 2 − 2 ⋅ r a n k i − 1 ( v ) = 2 ⋅ ( r a n k i ( v ) − r a n k i − 1 ( v ) )
同向双旋(zig-zig / zag-zag),( log G i + log V i − 1 ) / 2 ≤ log ( ( G i + V i − 1 ) / 2 ) < log ( V i / 2 ) (\log G_i + \log V_{i - 1}) / 2 \le \log ((G_i + V_{i - 1}) / 2) < \log (V_i / 2) ( log G i + log V i − 1 ) / 2 ≤ log ( ( G i + V i − 1 ) / 2 ) < log ( V i / 2 )
A i ( k ) = T i ( k ) + Δ Φ i ( k ) = 2 + Δ r a n k i ( g ) + Δ r a n k i ( p ) + Δ r a n k i ( v ) = 2 + [ r a n k i ( g ) − r a n k i − 1 ( g ) ] + [ r a n k i ( p ) − r a n k i − 1 ( p ) ] + [ r a n k i ( v ) − r a n k i − 1 ( v ) ] < 2 + r a n k i ( g ) + r a n k i ( p ) − 2 ⋅ r a n k i − 1 ( v ) < 2 + r a n k i ( g ) + r a n k i ( v ) − 2 ⋅ r a n k i − 1 ( v ) < 2 + 2 ⋅ r a n k i ( v ) − r a n k i − 1 ( v ) − 2 + r a n k i ( v ) − 2 ⋅ r a n k i − 1 ( v ) = 3 ⋅ ( r a n k i ( v ) − r a n k i − 1 ( v ) ) \begin{aligned} A^{(k)}_i &= T^{(k)}_i + \Delta\Phi^{(k)}_i = 2 + \Delta rank_i(g) + \Delta rank_i(p) + \Delta rank_i(v) \\ &= 2 + [rank_i(g) - \cancel{rank_{i - 1}(g)}] + [rank_i(p) - rank_{i - 1}(p)] + [\cancel{rank_i(v)} - rank_{i - 1}(v)] \\ &< 2 + rank_i(g) + rank_i(p) - 2 \cdot rank_{i - 1}(v) \\ &< 2 + rank_i(g) + rank_i(v) - 2 \cdot rank_{i - 1}(v) \\ &< 2 + 2 \cdot rank_i(v) - rank_{i - 1}(v) - 2 + rank_i(v) - 2 \cdot rank_{i - 1}(v) \\ &= 3 \cdot(rank_i(v) - rank_{i - 1}(v)) \end{aligned} A i ( k ) = T i ( k ) + Δ Φ i ( k ) = 2 + Δ r a n k i ( g ) + Δ r a n k i ( p ) + Δ r a n k i ( v ) = 2 + [ r a n k i ( g ) − r a n k i − 1 ( g ) ] + [ r a n k i ( p ) − r a n k i − 1 ( p ) ] + [ r a n k i ( v ) − r a n k i − 1 ( v ) ] < 2 + r a n k i ( g ) + r a n k i ( p ) − 2 ⋅ r a n k i − 1 ( v ) < 2 + r a n k i ( g ) + r a n k i ( v ) − 2 ⋅ r a n k i − 1 ( v ) < 2 + 2 ⋅ r a n k i ( v ) − r a n k i − 1 ( v ) − 2 + r a n k i ( v ) − 2 ⋅ r a n k i − 1 ( v ) = 3 ⋅ ( r a n k i ( v ) − r a n k i − 1 ( v ) )
单次伸展总复杂度为
A ( k ) = ∑ i A i ( k ) ≤ 3 ⋅ ∑ i ( r a n k i ( v ) − r a n k i − 1 ( v ) ) = 3 ⋅ ( r a n k ( r o o t ) − r a n k ( v ) ) ≤ 3 ⋅ log n = O ( log n ) \begin{aligned} A^{(k)} &= \sum_i A^{(k)}_i \le 3 \cdot \sum_i (rank_i(v) - rank_{i - 1}(v)) \\ &= 3 \cdot (rank(root) - rank(v)) \le 3 \cdot \log n = O(\log n) \end{aligned} A ( k ) = i ∑ A i ( k ) ≤ 3 ⋅ i ∑ ( r a n k i ( v ) − r a n k i − 1 ( v ) ) = 3 ⋅ ( r a n k ( r o o t ) − r a n k ( v ) ) ≤ 3 ⋅ log n = O ( log n )
B-树
分级存储:利用数据访问的局部性
常用的数据,复制到更高层、更小的存储器中
找不到,才向更低层、更大的存储器索取
缓存的体现: 就地 循环位移的倒置版本
1 2 3 4 5 void shift (int *A, int n, int k) reverse (A, k); reverse (A + k, n - k); reverse (A, n); }
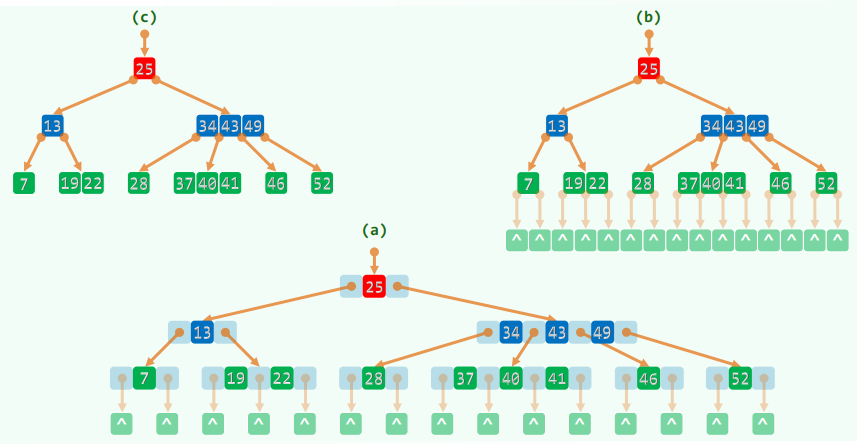
结构
外部节点+叶子
m m m m m m m ≥ 3 m \ge 3 m ≥ 3 外部节点的深度 统一相等 ,并以此深度作为树高 h h h
外部节点可看作 “可被插入的空隙”
叶节点的深度统一相等(h − 1 h - 1 h − 1
内部节点
各含有 n ≤ m − 1 n \le m - 1 n ≤ m − 1
各有 n + 1 ≤ m n + 1 \le m n + 1 ≤ m
反过来,分支数也不能太少
树根:2 ≤ n + 1 2 \le n + 1 2 ≤ n + 1
其余:⌈ m / 2 ⌉ ≤ n + 1 ≤ m \lceil m / 2 \rceil \le n + 1 \le m ⌈ m / 2 ⌉ ≤ n + 1 ≤ m
故亦称作 ( ⌈ m / 2 ⌉ , m ) (\lceil m / 2 \rceil, m) ( ⌈ m / 2 ⌉ , m )
查找
算法
从(常驻 RAM 的)根节点开始
只要当前节点不是外部节点
在当前节点中顺序查找(RAM 内部)
若找到目标关键码,则返回查找成功
否则,沿引用找到孩子节点,将其 读入内存
返回查找失败
实现
1 2 3 4 5 6 7 8 9 10 template <typename T> BTNodePosi<T> BTree<T>::search (T const &e) { _hot = NULL ; for (BTNodePosi<T> v = _root; v; ) { Rank r = v->key.search (e); if (r != -1 && (e == v->key[r])) return v; _hot = v; v = v->child[r + 1 ]; } return NULL ; }
性能
忽略内存中的查找,运行时间主要取决于 I/O 次数
在每一深度至多一次 I/O,故运行时间为 O ( log n ) O(\log n) O ( log n )
log m ( N + 1 ) ≤ h ≤ 1 + ⌊ log ⌈ m / 2 ⌉ N + 1 2 ⌋ \log_m (N + 1) \le h \le 1 + \lfloor \log_{\lceil m / 2 \rceil} \frac{N + 1}{2} \rfloor log m ( N + 1 ) ≤ h ≤ 1 + ⌊ log ⌈ m / 2 ⌉ 2 N + 1 ⌋
树最高的情况
对于内部节点,n k ≥ 2 × ⌈ m / 2 ⌉ k − 1 , ∀ k > 0 n_k \ge 2 \times \lceil m / 2 \rceil ^{k - 1}, \quad \forall k > 0 n k ≥ 2 × ⌈ m / 2 ⌉ k − 1 , ∀ k > 0
考察外部节点所在高度 h h h N + 1 = n h ≥ 2 × ⌈ m / 2 ⌉ h − 1 N + 1 = n_h \ge 2 \times \lceil m / 2 \rceil ^{h - 1} N + 1 = n h ≥ 2 × ⌈ m / 2 ⌉ h − 1
h ≤ 1 + ⌊ log ⌈ m / 2 ⌉ N + 1 2 ⌋ = O ( log m N ) h \le 1 + \lfloor \log_{\lceil m / 2 \rceil} \frac{N + 1}{2} \rfloor = O(\log_m N) h ≤ 1 + ⌊ log ⌈ m / 2 ⌉ 2 N + 1 ⌋ = O ( log m N )
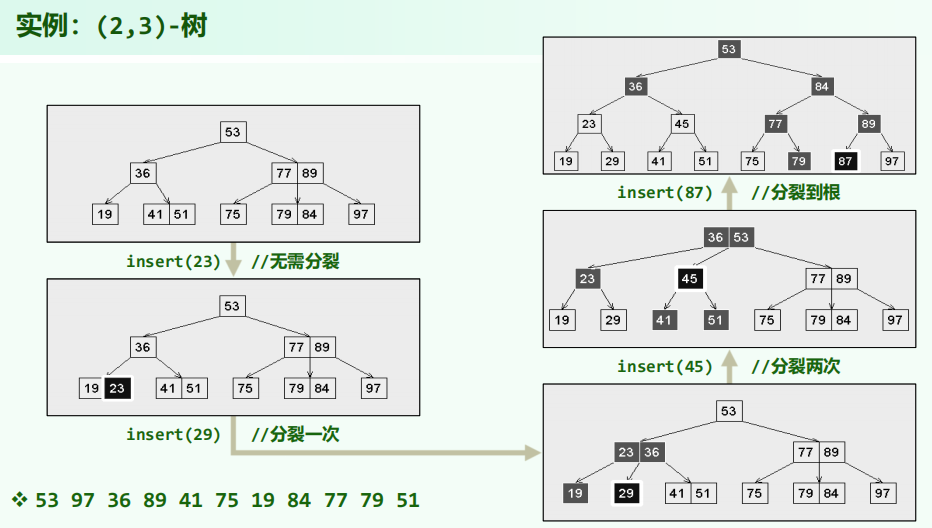
插入
1 2 3 4 5 6 7 8 9 template <typename T> bool BTree<T>::insert (const T &e) { BTNodePosi<T> v = search (e); if (v) return false ; Rank r = _hot->key.search (e); _hot->key.insert (r + 1 , e); _hot->child.insert (r + 2 , NULL ); _size++; solveOverflow (_hot); return true ; }
上溢修复
设上溢节点中的关键码依次为 { k 0 , k 1 , … , k m − 1 } \{k_0, k_1, \dots, k_{m - 1}\} { k 0 , k 1 , … , k m − 1 }
取中位数 s = ⌊ m / 2 ⌋ s = \lfloor m / 2 \rfloor s = ⌊ m / 2 ⌋ { k 0 , … , k s − 1 } \{k_0, \dots, k_{s - 1}\} { k 0 , … , k s − 1 } { k s } \{k_s\} { k s } { k s + 1 , … , k m − 1 } \{k_{s + 1}, \dots, k_{m - 1}\} { k s + 1 , … , k m − 1 }
关键码分裂,k s k_s k s
此时左、右孩子的关键码数目,均满足 m m m
若父节点本已饱和,则继续上溢
最坏情况 上溢持续 向上传播到根
此时可令最后被提升的关键码自成节点,作为新的根
B-树因此增高
总体执行时间正比于分裂次数,O ( h ) O(h) O ( h )
上溢也可采用旋转来修复
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 template <typename T> void BTree<T>::solveOverflow (BTNodePosi<T> v) { while (_m <= v->key.size ()) { Rank s = _m / 2 ; BTNodePosi<T> u = new BTNode <T>(); for (Rank j = 0 ; j < _m - s - 1 ; j++) { u->child.insert (j, v->child.remove (s + 1 )); u->key.insert (j, v->key.remove (s + 1 )); } u->child.insert[_m - s - 1 ] = v->child.remove (s + 1 ); if (u->child[0 ]) { for (Rank j = 0 ; j < _m - s; j++) u->child[j]->parent = u; } BTNodePosi<T> p = v->parent; if (!p) { _root = p = new BTNode <T>(); p->child[0 ] = v, v->parent = p; } Rank r = 1 + p->key.search (v->key[0 ]); p->key.insert (r, v->key.remove (s)); p->child.insert (r + 1 , u); u->parent = p; v = p; } }
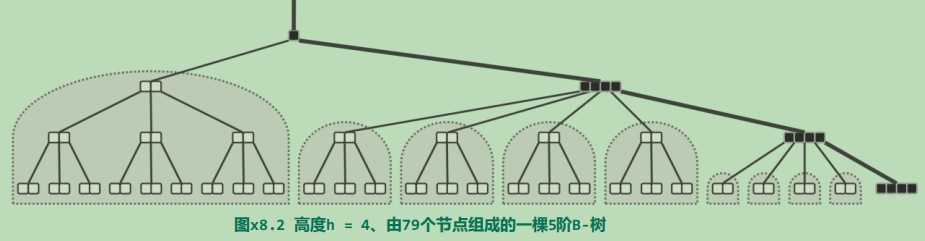
一棵存有 N N N m m m Θ ( log m N ) \Theta(\log_m N) Θ ( log m N )
全树总规模为 N ^ = ⌈ m / 2 ⌉ h − 1 + ( m − 1 ) ⋅ ( ⌈ m / 2 ⌉ h − 2 + ⌈ m / 2 ⌉ h − 3 + ⋯ + ⌈ m / 2 ⌉ 0 ) \hat{N} = \lceil m / 2 \rceil^{h - 1} + (m - 1) \cdot (\lceil m / 2 \rceil ^{h - 2} + \lceil m / 2 \rceil^{h-3} + \dots + \lceil m / 2 \rceil^{0}) N ^ = ⌈ m / 2 ⌉ h − 1 + ( m − 1 ) ⋅ ( ⌈ m / 2 ⌉ h − 2 + ⌈ m / 2 ⌉ h − 3 + ⋯ + ⌈ m / 2 ⌉ 0 )
对应高度可取为 h = 1 + log ⌈ m / 2 ⌉ ( ( N ^ ⋅ ( ⌈ m / 2 ⌉ − 1 ) + m − 1 ) / ( m + ⌈ m / 2 ⌉ − 2 ) ) = Θ ( log ⌈ m / 2 ⌉ N ^ ) = Θ ( log m N ^ ) \begin{aligned}h = 1 + \log_{\lceil m / 2 \rceil}((\hat{N} \cdot (\lceil m / 2 \rceil - 1) + m - 1) / (m + \lceil m / 2 \rceil - 2)) =\Theta(\log_{\lceil m / 2 \rceil} \hat{N}) = \Theta(\log_{m} \hat{N})\end{aligned} h = 1 + log ⌈ m / 2 ⌉ ( ( N ^ ⋅ ( ⌈ m / 2 ⌉ − 1 ) + m − 1 ) / ( m + ⌈ m / 2 ⌉ − 2 ) ) = Θ ( log ⌈ m / 2 ⌉ N ^ ) = Θ ( log m N ^ )
对于给定的 N N N h h h N ^ ≤ N \hat{N} \le N N ^ ≤ N
图示某一黑关键码和对应白关键码构成的 高度 为 k k k ⌈ m / 2 ⌉ k \lceil m / 2 \rceil^k ⌈ m / 2 ⌉ k
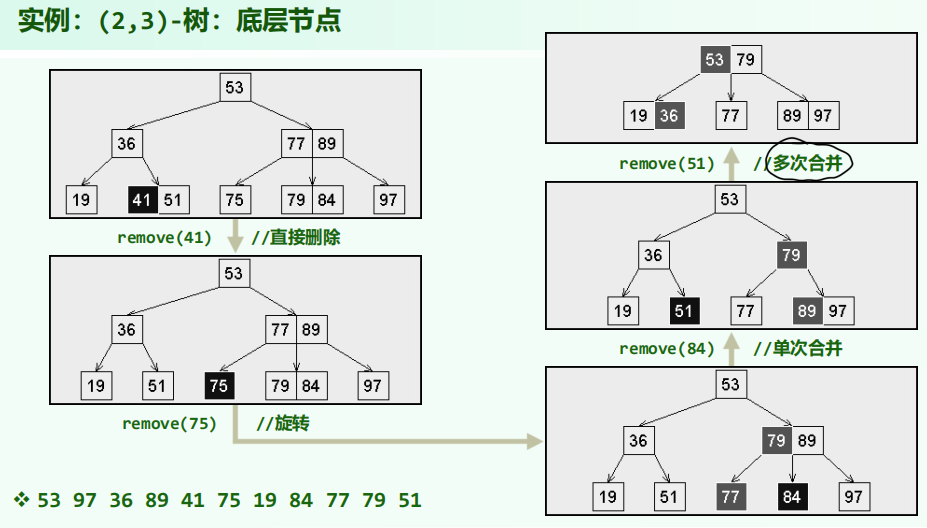
删除
若被删除元素非叶子,则先通过旋转 腾挪 (与后继交换),使其位于最底层
1 2 3 4 5 6 7 8 9 10 11 12 13 template <typename T> bool BTree<T>::remove (const T &e) { BTNodePosi<T> v = search (e); if (!v) return false ; Rank r = v->key.search (e); if (v->child[0 ]) { BTNodePosi<T> u = v->child[r + 1 ]; while (u->child[0 ]) u = u->child[0 ]; v->key[r] = u->key[0 ]; v = u, r = 0 ; } v->key.remove (r); v->child.remove (r + 1 ); _size--; solveUnderflow (); return true ; }
下溢修复
非根节点 v v v ⌈ m / 2 ⌉ − 2 \lceil m / 2 \rceil - 2 ⌈ m / 2 ⌉ − 2 ⌈ m / 2 ⌉ − 1 \lceil m / 2 \rceil - 1 ⌈ m / 2 ⌉ − 1
若左兄弟 L 存在,且至少包含 ⌈ m / 2 ⌉ \lceil m / 2 \rceil ⌈ m / 2 ⌉ 够借 )
将 P 中分界关键码 y y y
将 L 中最大关键码 x x x y y y
修复完成
若右兄弟 R 存在,且至少包含 ⌈ m / 2 ⌉ \lceil m / 2 \rceil ⌈ m / 2 ⌉
若 L 和 R 或不存在,或均不足 ⌈ m / 2 ⌉ \lceil m / 2\rceil ⌈ m / 2 ⌉
即便如此 L 和 R 必有其一,且恰含有 ⌈ m / 2 ⌉ − 1 \lceil m / 2 \rceil -1 ⌈ m / 2 ⌉ − 1
从 P 中抽出介于 L(R) 和 V 之间的关键码 y y y y y y
这可能导致 P 继续下溢,重复整个过程即可
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 template <typename T> void BTree<T>::solveUnderflow (BTNodePosi<T> v) { while ((_m + 1 ) / 2 > v->child.size ()) { BTNodePosi<T> p = v->parent; if (!p) { } Rank r = 0 ; while (p->child[r] != v) r++; if (r > 0 && (_m + 1 ) / 2 < p->child[r - 1 ]->child.size ()) { } else if (r < p->child.size () - 1 && (_m + 1 ) / 2 < p->child[r + 1 ]->child.size ()) { } else { if (r > 0 ) { } else { } } v = p; } }
红黑树
动机
并发性:对于 BST 而言,结构变化处需要加锁(产生访问延迟)
Splay 结构变化剧烈,最差 O ( n ) O(n) O ( n )
AVL 插入 O ( 1 ) O(1) O ( 1 ) O ( log n ) O(\log n) O ( log n )
持久性:支持对历史版本的访问
蛮力保存,单次操作 O ( log h + log n ) O(\log h + \log n) O ( log h + log n ) O ( n ⋅ h ) O(n \cdot h) O ( n ⋅ h )
压缩更新:大量共享,少量更新(仅支持对历史版本的读取)
每个版本的新增复杂度,仅为 O ( log n ) O(\log n) O ( log n )
可进一步提高至总体 O ( n + h ) O(n + h) O ( n + h ) O ( 1 ) O(1) O ( 1 )
为此,就树的 代数结构 而言,相邻版本之间的差异不能超过 O ( 1 ) O(1) O ( 1 )
结构
插入
按 BST 规则插入新关键码 e e e
除非是首个节点,否则 x x x p p p
先将 x x x
但可能出现双红,此时考查
祖父 g = p->parent 必存在且为黑
叔父 u = uncle(x) = sibling(p) ,无非两种情况
1 2 3 4 5 6 7 8 template <typename T> BinNodePosi<T> RedBlack<T>::insert (const T &e) { BinNodePosi<T> &x = search (e); if (x) return x; x = new BinNode <T>(e, _hot, NULL , NULL , 0 ); _size++; BinNodePosi<T> xOld = x; solveDoubleRed (x); return xOld; }
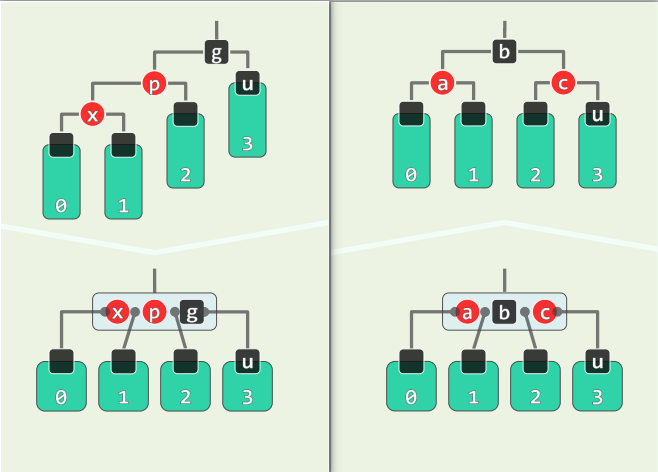
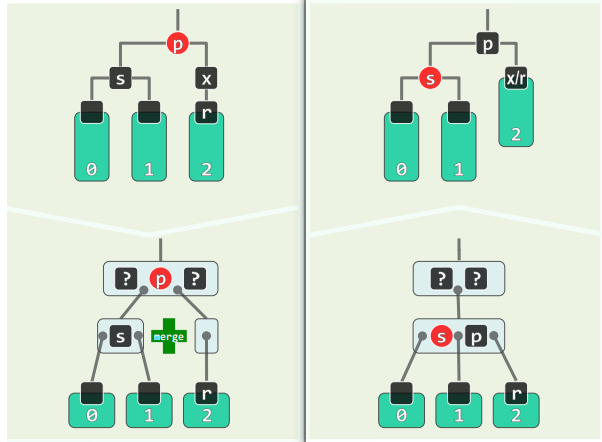
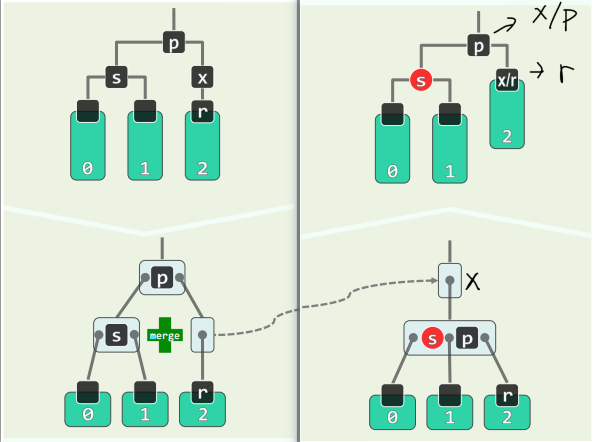
双红修正
RR-1: u->color = B
此时,x、p、g 的四个孩子(可能是外部节点)全黑,且黑高度相同
可进行局部“3+4”重构,b 转黑,a 或 c 转红
从 B-树的角度,相当于原三叉节点插入红关键码后,原黑关键码不再居中
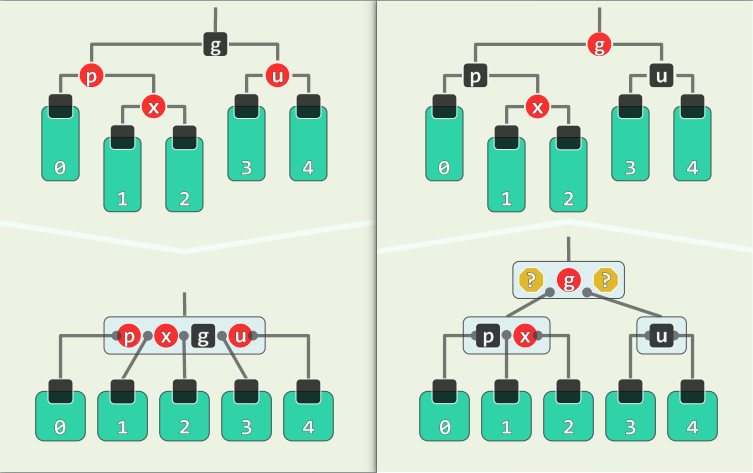
RR-2: u->color = R
等效于在 B-树中,超级节点发生上溢
故可以让 p 和 u 转黑,g 转红
等效于 节点分裂,关键码 g 上升一层
所以可能将双红向上传播
继续如法炮制即可
直至不再双红,或抵达树根(整树黑高度+1)
复杂度
重构、染色均只需常数时间
故 RedBlack::insert() 仅需 O ( log n ) O(\log n) O ( log n )
期间至多 O ( log n ) O(\log n) O ( log n ) O ( 1 ) O(1) O ( 1 )
分摊意义下,重染色次数为 O ( 1 ) O(1) O ( 1 )
旋转
染色
此后
u 为黑
1~2
2
调整随即完成
u 为红
0
3
可能再次双红,但必上升两层
删除
首先按 BST 常规算法进行删除 r = removeAt(x, _hot)
x 由其孩子 r 接替 ,此时另一孩子 k 必为 NULL
但实际调整过程中,x 可能逐层上升
故等效地理解为,k 是一棵 黑高度 与 r 相等的子树
此时条件 1、2 依然满足,但条件 3、4 未必
其一为红
若 x 为红,则 3、4 自然满足
若 r 为红,则令其与 x 交换颜色 即可
若 x 和 r 均黑,则此时全树黑深度不再统一
等效于 B-树中 x 所属节点发生下溢
在 新树 中,考查 r 的父亲,兄弟
1 2 p = r->parent; s = sibling (r);
无非四种情况,分别处理
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 template <typename T> bool RedBlack<T>::remove (const T &e) { BinNodePosi<T> &x = search (e); if (!x) return false ; BinNodePosi<T> r = removeAt (x, _hot); if (!(--_size)) return true ; if (!_hot) { _root->color = RB_BLACK; _root->updateHeight (); return true ; } if (BlackHeightUpdated (_hot)) return true ; if (IsRed (r)) { r->color = RB_BLACK; r->height++; return true ; } solveDoubleBlack (r); return true ; }
双黑修正
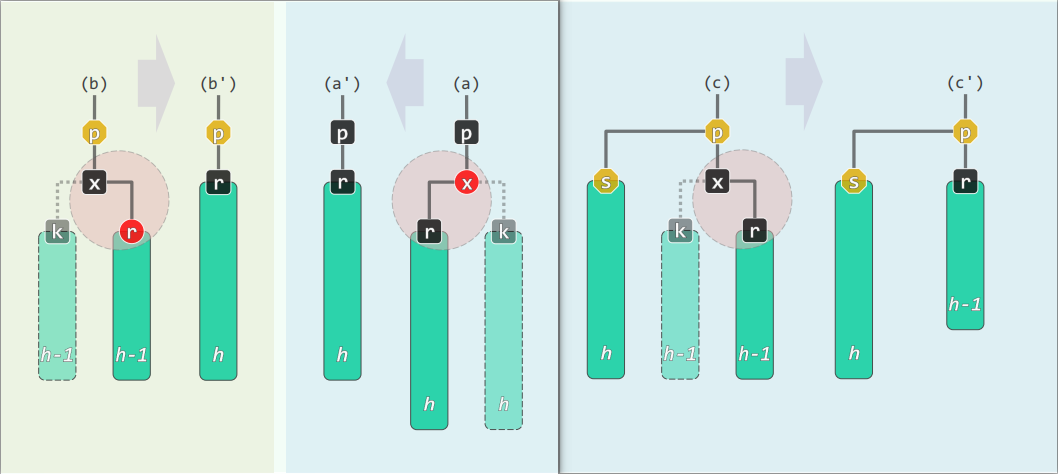
BB-1
s 为黑,且至少有一个红孩子 t
进行“3+4”重构,r 保持黑,a、c 染黑,b 继承 p 的原色
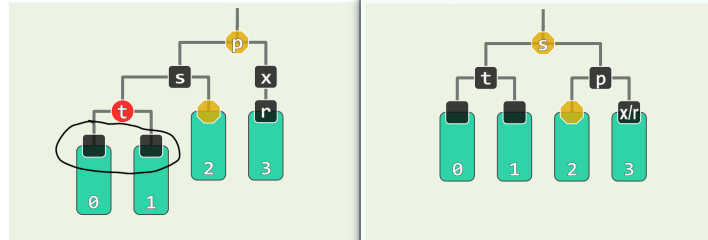
BB-2R
s 为黑,且两个孩子均为黑;p 为红
r 保持黑,s 转红,p 转黑
等效于下溢节点与兄弟节点合并
同时因为 p 左右还有黑关键码,不会导致下溢传播
BB-2B
s 为黑,且两个孩子均为黑;p 为黑
r 保持黑,s 转红,p 转黑
也等效于下溢节点与兄弟节点合并
但合并前,p 和 s 均属于单关键码节点,故 父节点继续下溢
继续处理即可,至多 O ( log n ) O(\log n) O ( log n )
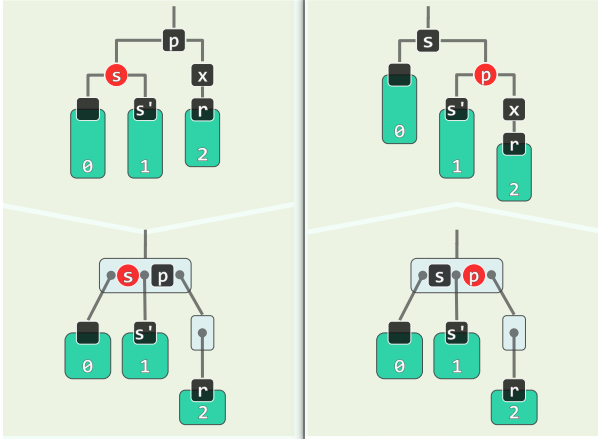
BB-3
s 为红(其孩子均为黑)
绕 p 单旋,s 由红转黑,p 由黑转红
黑高度依然异常,但 r 有了新的(黑)兄弟
且由于 p 转红,接下来的情况变为 BB-1 或 BB-2R
再调整一轮,即可恢复
道理是“存在红色就可以在子树中腾挪”,但需要先调整一下形态
想在红黑树的等效 B-树节点中交换节点颜色(即在 B-树中改变与上层节点的联接),需要进行旋转
复杂度
RedBlack<T>::remove 仅需 O ( log n ) O(\log n) O ( log n )
期间至多 O ( log n ) O(\log n) O ( log n ) O ( 1 ) O(1) O ( 1 )
分摊意义下,重染色次数为 O ( 1 ) O(1) O ( 1 )
旋转
染色
此后
(1)黑 s 有红子 t
1~2
3
调整随即完成
(2R)黑 s 无红子,p 红
0
2
调整随即完成
(2B)黑 s 无红子,p 黑
0
1
必再次双黑,但上升一层
(3)红 s
1
2
转为(1)或(2R)
词典
散列
循对象访问
entry = (key, value)关键码未必可定义大小(但可判等),查找对象不限于最大/最小词条
散列表/散列函数
桶(bucket):直接存放或间接指向一个词条
Bucket array ∼ \sim ∼
容量:M \mathcal{M} M
满足:N < M ≪ R \mathcal{N} < \mathcal{M} \ll \mathcal{R} N < M ≪ R
空间:O ( N + M ) = O ( N ) \mathcal{O}(\mathcal{N} + \mathcal{M}) = \mathcal{O}(\mathcal{N}) O ( N + M ) = O ( N )
定址
根据词条的 key(未必可比较), “直接”确定散列表入口 (无论表有多长)
散列函数
hash(): $ key \rightarrow &entry$如 hash(key) = key % M
“直接”:e x p e c t e d − O ( 1 ) expected-O(1) e x p e c t e d − O ( 1 )
冲突
散列函数
评价和设计原则
确定:同一关键码总是被映射至 同一 位置
快速:e x p e c t e d − O ( 1 ) expected-O(1) e x p e c t e d − O ( 1 )
满射:尽可能充分利用整个散列空间
均匀:关键码映射到散列表各位置的概率尽量接近
基本
除余法
h a s h ( k e y ) = k e y % M hash(key) = key \, \% \, M h a s h ( k e y ) = k e y % M
据说 M M M
序列的 Kolmogorov \text{Kolmogorov} Kolmogorov
实际应用中的数据序列 远非理想随机
面对往往具有周期的词条,将 散列表长 取作素数,可将 聚集 之概率降至最低
MAD 法
除余法的缺陷
不动点:无论表长 M M M h a s h ( 0 ) ≡ 0 hash(0) \equiv 0 h a s h ( 0 ) ≡ 0
相关性:虽然 [ 0 , R ) [0, R) [ 0 , R ) M M M 相邻 关键码的散列地址也必相邻
Multiply-Add-Divide
h a s h ( k e y ) = ( a × k e y + b ) % M , M prime , a > 1 , b > 0 , M ∤ a hash(key) = (a \times key + b) \% M, \, M \, \text{prime}, a > 1, b > 0, M \nmid a h a s h ( k e y ) = ( a × k e y + b ) % M , M prime , a > 1 , b > 0 , M ∤ a
更多
平方取中/mid-square
折叠法
位异或法
总之,越是随机,越是 没有规律 ,越好
随机数
(伪)随机数法
径取:h a s h ( k e y ) = r a n d ( k e y ) = [ r a n d ( 0 ) × a k e y ] % M hash(key) = rand(key) = [rand(0) \times a^{key}] \% M h a s h ( k e y ) = r a n d ( k e y ) = [ r a n d ( 0 ) × a k e y ] % M
种子:r a n d ( 0 ) rand(0) r a n d ( 0 )
1 2 3 4 5 6 unsigned long int next = 1 ;void srand (unsigned int seed) int rand (void ) next = next * 1103515425 + 12345 ; return (unsigned int ) (M / 65536 ) % 32768 ; }
就地随机置乱
任给一个数组 A [ 0 , n ) A[0, n) A [ 0 , n )
1 2 3 4 void shuffle (int A[], int n) for (; n > 1 ; n--) swap (A[rand () % M], A[n - 1 ]); }
hashCode 与多项式法
1 2 3 4 5 6 7 8 static Rank hashCode (char s[]) Rank n = strlen (s); Rank h = 0 ; for (Rank i = 0 ; i < n; i++) { h = (h << 5 ) | (h >> 27 ); h += s[i]; } return h; }
排解冲突
开放散列
多槽位
独立链
每个桶拥有一个列表,存放对应的一组同义词
优点
缺点
耗费更多空间和时间
空间未必连续分布,缓存难以生效
两个结论
在 简单均匀 散列的假设下,对于使用 独立链 法解决冲突的散列表
装填因子 λ = n m \lambda = \frac{n}{m} λ = m n λ \lambda λ
故一次不成功的查找平均要检查 λ \lambda λ Θ ( 1 + λ ) \Theta(1 + \lambda) Θ ( 1 + λ )
而对于成功查找,考虑顺序插入的 n n n k 1 , k 2 , … , k n k_1, k_2, \dots, k_n k 1 , k 2 , … , k n
根据简单均匀散列假设,任意两个关键字被插入同一链条的概率为 1 m \frac{1}{m} m 1
对于 k i k_i k i k i k_i k i n − i m \frac{n - i}{m} m n − i
故总期望查找时间为 1 n ∑ i = 1 n ( 1 + n − i m ) = 1 + 1 n m ∑ i = 1 n ( n − i ) = 1 + 1 n m [ n 2 − n ( n + 1 ) 2 ] = 1 + n − 1 2 m = 1 + λ 2 − λ 2 n \begin{aligned} \frac{1}{n}\sum_{i = 1}^n(1 + \frac{n - i}{m}) &= 1 + \frac{1}{nm} \sum_{i = 1}^n (n - i) \\ &= 1 + \frac{1}{nm}[n^2 - \frac{n(n + 1)}{2}] \\ &= 1 + \frac{n - 1}{2m} = 1 + \frac{\lambda}{2} - \frac{\lambda}{2n} \end{aligned} n 1 i = 1 ∑ n ( 1 + m n − i ) = 1 + n m 1 i = 1 ∑ n ( n − i ) = 1 + n m 1 [ n 2 − 2 n ( n + 1 ) ] = 1 + 2 m n − 1 = 1 + 2 λ − 2 n λ
因此总平均时间(包括计算散列函数的时间)为 Θ ( 2 + λ 2 − λ 2 n ) = Θ ( 1 + λ ) \Theta(2 + \frac{\lambda}{2} - \frac{\lambda}{2n}) = \Theta(1 + \lambda) Θ ( 2 + 2 λ − 2 n λ ) = Θ ( 1 + λ )
公共溢出区
单独开辟一块连续空间,发生冲突的词条,顺序存入此区域
结构简单易于实现
一旦发生冲突,最坏情况下,处理冲突的时间将正比于溢出区的规模
封闭散列
封闭散列:散列表的物理空间相对固定,所有冲突都在 内部 寻求解决
开放定址 (≠ \ne = 试探链(Probe Chain):为每一组同义词,都 事先约定了若干备用桶 ,一次串接成序列/链
查找算法:沿试探链逐个检视,直到命中成功,或抵达空桶而失败
相对于开放散列,整体结构更加整饬,cache 机制易生效
给定一个装填因子 λ = n m < 1 \lambda = \frac{n}{m} < 1 λ = m n < 1
一次不成功的查找,期望探查次数至多为 1 1 − λ \frac{1}{1 - \lambda} 1 − λ 1
一次成功的查找,期望探查次数至多为 1 λ ln 1 1 − λ \frac{1}{\lambda} \ln \frac{1}{1 - \lambda} λ 1 ln 1 − λ 1
在一次不成功的查找(最后一次槽为空)中,令 X X X
对于 i > 1 i > 1 i > 1 i − 1 i - 1 i − 1 i i i n − i + 1 m − i + 1 \frac{n - i + 1}{m - i + 1} m − i + 1 n − i + 1
则 Pr { X ≥ i } = n m ⋅ n − 1 m − 1 ⋅ n − 2 m − 2 ⋯ n − i + 2 m − i + 2 ≤ ( n m ) i − 1 \Pr\{X \ge i\} = \frac{n}{m} \cdot \frac{n - 1}{m - 1} \cdot \frac{n - 2}{m - 2} \cdots \frac{n - i + 2}{m - i + 2} \le (\frac{n}{m})^{i - 1} Pr { X ≥ i } = m n ⋅ m − 1 n − 1 ⋅ m − 2 n − 2 ⋯ m − i + 2 n − i + 2 ≤ ( m n ) i − 1
E [ X ] = ∑ i = 1 ∞ i ⋅ Pr { X = i } = ∑ i = 1 ∞ Pr { X ≥ i } ≤ ∑ i = 1 ∞ λ i − 1 = 1 1 − λ \begin{aligned}E[X] = \sum_{i=1}^\infty i \cdot \Pr\{X = i\} = \sum_{i = 1}^\infty \Pr\{X \ge i\} \le \sum_{i = 1}^\infty \lambda^{i - 1} = \frac{1}{1 -\lambda} \end{aligned} E [ X ] = i = 1 ∑ ∞ i ⋅ Pr { X = i } = i = 1 ∑ ∞ Pr { X ≥ i } ≤ i = 1 ∑ ∞ λ i − 1 = 1 − λ 1
对第 i + 1 i + 1 i + 1 k k k 1 1 − i / m = m m − i \frac{1}{1 - i / m} = \frac{m}{m - i} 1 − i / m 1 = m − i m
1 n ∑ i = 0 n − 1 m m − i = 1 λ ∑ k = m − n + 1 m 1 k ≤ 1 λ ∫ m − n m ( 1 / x ) d x = 1 λ ln 1 1 − λ \begin{aligned}\frac{1}{n}\sum_{i = 0}^{n - 1}\frac{m}{m - i} = \frac{1}{\lambda} \sum_{k = m - n + 1}^m \frac{1}{k} \le \frac{1}{\lambda} \int_{m-n}^{m} (1/x)\, {\rm d}x = \frac{1}{\lambda} \ln \frac{1}{1 - \lambda} \end{aligned} n 1 i = 0 ∑ n − 1 m − i m = λ 1 k = m − n + 1 ∑ m k 1 ≤ λ 1 ∫ m − n m ( 1 / x ) d x = λ 1 ln 1 − λ 1
线性试探
r i ( k e y ) = ( hash ( k e y ) + i ) mod M , i = 0 , 1 , 2 , 3 , … r_i(key) = (\text{hash}(key) + i) \, \text{mod} \, \mathcal{M}, \quad i = 0, 1, 2, 3, \dots r i ( k e y ) = ( hash ( k e y ) + i ) mod M , i = 0 , 1 , 2 , 3 , … 只要还有空桶,试探链就不会循环,查找也能终止
试探链会相互重叠,非同义词会彼此堆积
控制好装填因子,冲突和堆积都不致太严重:E ( p r o b e s ) = 1 1 − λ E(probes) = \frac{1}{1 - \lambda} E ( p r o b e s ) = 1 − λ 1
数据局部性极佳,系统缓存的作用发挥极致
对于一个装填因子为 λ = n m \lambda = \frac{n}{m} λ = m n A S L s u c c ∼ 1 2 ( 1 + 1 1 − λ ) ASL_{succ}\sim \frac{1}{2}(1 + \frac{1}{1 - \lambda}) A S L s u c c ∼ 2 1 ( 1 + 1 − λ 1 ) A S L f a i l ∼ 1 2 ( 1 + 1 ( 1 − λ ) 2 ) ASL_{fail}\sim \frac{1}{2}(1 + \frac{1}{(1 - \lambda)^2}) A S L f a i l ∼ 2 1 ( 1 + ( 1 − λ ) 2 1 )
对于一组固定的键,它们的总探查次数是一个固定值,与插入顺序无关
懒惰删除
仅做标记,不对试探链做更多调整
Bitmap *removed;查找时,被视为“必不匹配的非空桶 ”,使得试探链可以在此 延续
插入时,被视作“总是匹配的空闲桶 ”,以存放新词条
装填因子的计算口径有变
试探链因此可能彼此有所重叠
任何一个带有懒惰删除标记的桶,都可能同时属于多个试探链
1 2 3 4 5 6 7 8 9 10 11 template <typename K, typename V> Rank Hashtable<K, V>::probe4Hit (const K &k) { for (Rank r = hashCode (k) % M; ; r = (r + 1 ) % M) if (ht[r] && (k == ht[r]->key) || !ht[r] && !removed->test (r)) { return r; } } template <typename K, typename V> Rank Hashtable<K, V>::probe4Free (const K &k) { for (Rank r = hashCode (k) % M; ; r = (r + 1 ) % M) if (!ht[r]) return r; }
重散列
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 template <typename K, typename V> bool Hashtable<K, V>::remove (K k) { Rank r = prob4Hit (k); if (!ht[r]) return false ; delete ht[r]; ht[r] = NULL ; --N; removed->set (r); return true ; } template <typename K, typename V> bool Hashtable<K, V>::put (K k, V v) { if (ht[probe4Hit (k)]) return false ; Rank r = probe4Free (k); ht[r] = new Entry <K, V>(k, v); ++N; removed->clear (r); if ((N + removed->size ()) * 2 > M) rehash (); return true ; }
Rehashing:随着装填因子攀升,冲突激增;超过阈值后,便需要扩容
1 2 3 4 5 6 7 8 9 10 11 template <typename K, typename V> void Hashtable<K, V>::rehash () { Rank oldM = M; Entry<K, V> **oldHt = ht; ht = new Entry<K, V> *[M = primeNLT (4 * N)]; N = 0 ; memset (ht, 0 , sizeof (Entry<K,V>*) * M); delete removed; removed = new Bitmap (M); for (Rank i = 0 ; i < oldM; i++) if (oldHt[i]) put (oldHt[i]->key, oldHt[i]->value); delete [] oldHt; }
平方试探
r i ( k e y ) = ( h a s h ( k e y ) + i 2 ) m o d M , i = 0 , 1 , 2 , 3 , … r_i(key) = ({\rm hash}(key) + i^2) \, {\rm mod} \, M, \quad i = 0, 1, 2, 3, \dots r i ( k e y ) = ( h a s h ( k e y ) + i 2 ) m o d M , i = 0 , 1 , 2 , 3 , … 数据堆积现象改善,cache 利用率下降但依旧够用
表长为 素数 (不仅限于)时,只要 λ < 0.5 \lambda < 0.5 λ < 0 . 5
若 M M M n 2 % M n^2 \, \% \,M n 2 % M 恰有 ⌈ M / 2 ⌉ \lceil M / 2 \rceil ⌈ M / 2 ⌉ 前 ⌈ M / 2 ⌉ \lceil M / 2 \rceil ⌈ M / 2 ⌉
反证,假设存在 0 ≤ a < b < ⌈ M / 2 ⌉ 0 \le a < b < \lceil M / 2 \rceil 0 ≤ a < b < ⌈ M / 2 ⌉ a a a b b b
则有 a 2 ≡ b 2 ( m o d M ) a^2 \equiv b^2 \quad({\rm mod} \, M) a 2 ≡ b 2 ( m o d M ) ( b + a ) ⋅ ( b − a ) ≡ 0 ( m o d M ) (b + a) \cdot (b - a) \equiv 0 \quad ({\rm mod} \, M) ( b + a ) ⋅ ( b − a ) ≡ 0 ( m o d M )
然而,0 < b − a ≤ b + a < ⌈ M / 2 ⌉ + ( ⌈ M / 2 ⌉ − 1 ) ≤ ⌈ M / 2 ⌉ + ⌊ M / 2 ⌋ = M 0 < b - a \le b + a < \lceil M / 2 \rceil + (\lceil M / 2 \rceil - 1) \le \lceil M / 2 \rceil + \lfloor M / 2 \rfloor = M 0 < b − a ≤ b + a < ⌈ M / 2 ⌉ + ( ⌈ M / 2 ⌉ − 1 ) ≤ ⌈ M / 2 ⌉ + ⌊ M / 2 ⌋ = M
无论 b − a b - a b − a b + a b + a b + a M M M
双向平方试探
r i ( k e y ) = ( h a s h ( k e y ) + ( − 1 ) i + 1 ⋅ ( ⌈ i / 2 ⌉ ) 2 ) m o d M , i = 0 , 1 , 2 , 3 , … r_i(key) = ({\rm hash}(key) + (-1)^{i + 1} \cdot (\lceil i / 2 \rceil)^2) \, {\rm mod} \, M, \quad i = 0, 1, 2, 3, \dots r i ( k e y ) = ( h a s h ( k e y ) + ( − 1 ) i + 1 ⋅ ( ⌈ i / 2 ⌉ ) 2 ) m o d M , i = 0 , 1 , 2 , 3 , … 正向和反向的子试探链,各自包含 ⌈ M / 2 ⌉ \lceil M / 2 \rceil ⌈ M / 2 ⌉
− ⌊ M / 2 ⌋ , … , − 2 , − 1 , 0 , 1 , 2 , … , ⌊ M / 2 ⌋ -\lfloor M / 2 \rfloor, \dots, -2, -1, 0, 1, 2, \dots, \lfloor M / 2 \rfloor − ⌊ M / 2 ⌋ , … , − 2 , − 1 , 0 , 1 , 2 , … , ⌊ M / 2 ⌋ 表长取 素数 M = 4 ⋅ k + 3 \mathcal{M} = 4 \cdot k + 3 M = 4 ⋅ k + 3 (但不仅限于这些数),则 必然 可以保证试探链的前 M M M
原理:素数 p p p p ≡ 3 ( m o d 4 ) p \equiv 3 ({\rm mod} \, 4) p ≡ 3 ( m o d 4 )
双散列
预先约定第二散列函数:h a s h 2 ( k e y , i ) hash_2(key, i) h a s h 2 ( k e y , i )
冲突时,由其确定偏移增量,确定下一试探位置
( h a s h ( k e y ) + ∑ i = 1 k h a s h 2 ( k e y , i ) ) % M \begin{aligned}(hash(key) + \sum_{i = 1}^k hash_2(key, i)) \, \% \, M\end{aligned} ( h a s h ( k e y ) + i = 1 ∑ k h a s h 2 ( k e y , i ) ) % M
线性试探:h a s h 2 ( k e y , i ) ≡ 1 hash_2(key, i) \equiv 1 h a s h 2 ( k e y , i ) ≡ 1
平方试探:h a s h 2 ( k e y , i ) = 2 i − 1 hash_2(key, i) = 2i - 1 h a s h 2 ( k e y , i ) = 2 i − 1
桶排序
算法
简单情况
对 [ 0 , m ) [0, m) [ 0 , m ) n n n < m <m < m H[] 进行排序
空间 O ( m ) O(m) O ( m ) O ( m ) O(m) O ( m )
复杂情况
允许相等的元素(可能 m ≪ n m \ll n m ≪ n
依然使用散列表,每一组同义词各成一个链表
空间 O ( n + m ) O(n + m) O ( n + m ) O ( n ) O(n) O ( n )
Max Gap
任意 n n n n − 1 n - 1 n − 1
排序再计算—— O ( n log n ) O(n \log n) O ( n log n )
采用分桶策略,可改进至 O ( n ) O(n) O ( n )
线性算法
一趟扫描找到最左、最右点
将有效范围 均等 划分为 n − 1 n - 1 n − 1 n n n
通过散列,将各点归入对应的桶
计算相邻 非空 桶之间的“距离”
最大距离即 Max Gap
正确性:由于有 n n n n n n 至少跨越两个桶
对称的 Mini Gap 问题 不能 沿用该法突破 Ω ( n log n ) \Omega(n \log n) Ω ( n log n )
基数排序
有时,关键码由多个域(字段)组合而成:k t , k t − 1 , … , k 1 k_t, k_{t - 1}, \dots, k_1 k t , k t − 1 , … , k 1
可以采用 低位优先的多趟桶排序 ——基数排序
自 k 1 k_1 k 1 k t k_t k t
总时间为 O ( n + M 1 ) + O ( n + M 2 ) + ⋯ + O ( n + M t ) = O ( t × ( n + M ) ) O(n + M_1) + O(n + M_2) + \dots + O(n + M_t) = O(t \times (n + M)) O ( n + M 1 ) + O ( n + M 2 ) + ⋯ + O ( n + M t ) = O ( t × ( n + M ) )
常对数密度整数集
考查取自 [ 0 , n d ) [0, n^d) [ 0 , n d ) n n n ln n ln n d = 1 d = O ( 1 ) \frac{\ln n}{\ln n^d} = \frac{1}{d} = O(1) l n n d l n n = d 1 = O ( 1 )
此时可将所有元素预处理为 n n n
x = ( x d , … , x 3 , x 2 , x 1 ) x = (x_d, \dots, x_3, x_2, x_1) x = ( x d , … , x 3 , x 2 , x 1 ) 每个元素均转化为 d d d
排序时间为 d ⋅ ( n + n ) = O ( n ) = o ( n log n ) d \cdot (n + n) = O(n) = o(n \log n) d ⋅ ( n + n ) = O ( n ) = o ( n log n )
计数排序
原理
统计每个数出现次数
自前向后扫描各桶,依次累加
自后向前 计算每个数的排名
对应桶的计数减一,即是其在最终有序序列中对应的秩
不可改为从前向后扫描,否则稳定性无法保证
时间复杂度 O ( n + m ) O(n + m) O ( n + m ) O ( n + m ) O(n + m) O ( n + m )
跳转表
结构
逐层 折半稀疏 的列表:S 0 , S 1 , … , S h S_0, S_1, \dots, S_h S 0 , S 1 , … , S h
依次叠放耦合,S 0 S_0 S 0 S h S_h S h
横向为层 level :prev() 、next() 、哨兵
纵向成塔 tower :above() 、below()
四联节点
空间性能 e x p e c t e d {\rm expected} e x p e c t e d O ( n ) O(n) O ( n )
S 0 S_0 S 0 S k S_k S k p k p^{k} p k 第 k k k E ( ∣ S k ∣ ) = n ⋅ p k E(\left\vert S_k \right\vert) = n \cdot p^{k} E ( ∣ S k ∣ ) = n ⋅ p k
所有节点期望总数为 E ( ∑ k ∣ S k ∣ ) = n × ∑ k p k = n 1 − p = O ( n ) E(\sum_k \left\vert S_k \right\vert) = n \times \sum_k p^{k} = \frac{n}{1 - p} = O(n) E ( ∑ k ∣ S k ∣ ) = n × ∑ k p k = 1 − p n = O ( n )
查找、插入和删除
1 2 3 4 5 6 7 8 template <typename K, typename V> QNodePosi<Entry<K, V>> Skiplist<K, V>::search (K k) { for (QNodePosi<Entry<K, V>> p = first ()->data->head; ; ) { if (p->succ->succ && (p->succ->entry.key <= k)) p = p->succ; else if (p->below) p = p->below; else return p; } }
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 template <typename K, typename V> bool Skiplist<K, V>::put (K k, V v) { Entry<K, V> e = Entry <K, V>(k, v); QNodePosi<Entry<K, V>> p = search (k); ListNodePosi<Quadlist<Entry<K, V>>* > qlist = last (); QNodePosi<Entry<K, V>> b = qlist->data->insert (e, p); while (rand () & 1 ) { while (p->pred && !p->above) p = p->pred; if (!p->pred && !p->above) { insertFirst (new Quadlist<Entry<K, V>>); first ()->data->head ()->below = qlist->data->head; qlist->data->head->above = first ()=>data->head; } p = p->above; qlist = qlist->pred; b = qlist->data->insert (e, p, b); } return true ; }
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 template <typename K, typename V> bool Skiplist<K, V>::remove (K k) { QNodePosi<Entry<K, V>> p = search (k); if (!p->pred || (k != p->entry.key)) return false ; ListNodePosi<Quadlist<Entry<K, V>> *> qlist = last (); while (p->above) { qlist = qlist->pred; p = p->above; } do { QNodePosi<Entry<K, V>> lower = p->below; qlist->data->remove (p); p = lower; qlist = qlist->succ; } while (qlist->succ); while (height () > 1 && first ()->data->_size < 1 ) { List::remove (first ()); first ()->data->head->above = NULL ; } return true ; }
总览
纵向跳转 ∼ \sim ∼
一座塔的高度不低于 k k k p k p^k p k
Pr ( ∣ S k ∣ = 0 ) = ( 1 − p k ) n ≥ 1 − n ⋅ p k \Pr(\left\vert S_k \right\vert = 0) = (1 - p^k)^n \ge 1 - n \cdot p^k Pr ( ∣ S k ∣ = 0 ) = ( 1 − p k ) n ≥ 1 − n ⋅ p k 跳转表高度 h = log 1 / p ( n ) = O ( log n ) h = \log_{1/p}(n) = O(\log n) h = log 1 / p ( n ) = O ( log n )
查找过程中,纵向 跳转的次数,累计不过 e x p e c t e d {\rm expected} e x p e c t e d O ( log n ) O(\log n) O ( log n )
单个塔高为 e x p e c t e d {\rm expected} e x p e c t e d O ( 1 ) O(1) O ( 1 )
横向跳转 ∼ \sim ∼
在同一水平列表中,横向跳转所经节点必然依次紧邻,而且每次抵达都是 塔顶
将沿同一层列表跳转的次数记作 Y Y Y 几何分布 (简化模型,最后一个也可能是塔顶)
Pr ( Y = k ) = ( 1 − p ) k ⋅ p \Pr(Y=k) = (1 - p)^k \cdot p Pr ( Y = k ) = ( 1 − p ) k ⋅ p E ( Y ) = ( 1 − p ) / p E(Y) = (1 - p) / p E ( Y ) = ( 1 − p ) / p
因此,对于 p = 1 / 2 p = 1/2 p = 1 / 2
跳转表的每次查找,都可在 ≤ e x p e c t e d − ( 2 h ) = e x p e c t e d − O ( log n ) \le expected-(2h) = expected-O(\log n) ≤ e x p e c t e d − ( 2 h ) = e x p e c t e d − O ( log n )
通过维护每一个前向指针的长度,还可以将跳表的随机访问优化至 O ( log n ) O(\log n) O ( log n )
图
概述
G = ( V ; E ) G = (V; \, E) G = ( V ; E ) n = ∣ V ∣ n = \left\vert V \right\vert n = ∣ V ∣ e = ∣ E ∣ e = \left\vert E \right\vert e = ∣ E ∣ 同一条边的两个顶点 u 、 v u、v u 、 v ( u , v ) (u, v) ( u , v )
所有边均为方向的图为无向图
有向图中均为有向边 u → v u \rightarrow v u → v
u 、 v u、v u 、 v ( u , v ) (u, v) ( u , v ) 尾 、 头
路径 π = ⟨ v 0 , v 1 , … , v k ⟩ \pi = \left\langle v_0, v_1, \dots, v_k \right\rangle π = ⟨ v 0 , v 1 , … , v k ⟩ ∣ π ∣ = k \left\vert \pi \right\vert = k ∣ π ∣ = k
简单路径:v i ≠ v j v_i \ne v_j v i = v j i = j i = j i = j
环路:v 0 = v k v_0 = v_k v 0 = v k
欧拉环路:各边恰好出现一次
哈密尔顿环路:各点恰好出现一次
有向无环图:Directed Acyclic Graph,DAG
图 G = ( V ; E ) G = (V; \, E) G = ( V ; E ) T = ( V ; F ) T=(V; \, F) T = ( V ; F ) G G G 支撑树
各边 e e e w t ( e ) {\rm wt}(e) w t ( e )
同一网络的支撑树中,总权重最小者为最小支撑树(MST)
图的存储
模板类
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 template <typename Tv, typename Te> class Graph {private : void reset () for (Rank v = 0 ; v < n; v++) { status (v) = UNDISCOVERD; dTime (v) = fTime (v) = -1 ; parent (v) = -1 ; priority (v) = INT_MAX; for (Rank u = 0 ; u < n; u++) if (exists (v, u)) type (v, u) = UNDETERMINED; } } public : Rank n, e; } using VStatus = enum { UNDISCOVERED, DISCOVERED, VISITED };template <typename Tv> struct Vertex { Tv data; int inDegree, outDegree; VStatus status; int dTime, fTime; Rank parent; int priority; Vertex (Tv const &d) : data (d), inDegree (0 ), outDegree (0 ), status (UNDISCOVERED), dTime (-1 ), fTime (-1 ), parent (-1 ), priority (INT_MAX) {} }; using EType = enum { UNDETERMINED, TREE, CROSS, BACKWARD };template <typename Te> struct Edge { Te data; int weight; Etype type; Edge (Te const &d, int w) : data (d), weight (w), type (UNDETERMINED) {} };
邻接矩阵
Adjacency Matrix:记录顶点之间的 邻接 关系
矩阵元素 ⇔ \Leftrightarrow ⇔
若 v 、 u v、u v 、 u A ( v , u ) = 1 A(v, u) = 1 A ( v , u ) = 1
空间复杂度 Θ ( n 2 ) \Theta(n^2) Θ ( n 2 )
优点
直观,易于理解实现
尤其适用于稠密图
一些操作只需 O ( 1 ) O(1) O ( 1 )
缺点
Θ ( n 2 ) \Theta(n^2) Θ ( n 2 )
对于平面图 planar graph :可 嵌入 于平面的图
v − e + f − c = 1 , f o r a n y p g v - e + f - c = 1, \quad {\rm for \,\, any \,\, pg} v − e + f − c = 1 , f o r a n y p g
分别代表点数、边数、将平面分割成的区域数、联通分量
e ≤ 3 n − 6 = O ( n ) ≪ n 2 e \le 3n - 6 =O(n) \ll n^2 e ≤ 3 n − 6 = O ( n ) ≪ n 2
Incidence Matrix:记录顶点与边之间的关联关系
空间复杂度 Θ ( n ⋅ e ) = O ( n 3 ) \Theta(n \cdot e) = O(n^3) Θ ( n ⋅ e ) = O ( n 3 ) 2 e n e = 2 n → 0 \frac{2e}{ne} = \frac{2}{n} \rightarrow 0 n e 2 e = n 2 → 0
邻接表
将邻接矩阵的 各行 组织为列表,只记录存在的边
等效于,每一顶点 v v v L v = { u ∣ ⟨ v , u ⟩ ∈ E } L_v = \{u\, | \,\left\langle v, u \right\rangle \, \in E\} L v = { u ∣ ⟨ v , u ⟩ ∈ E }
有向图 O ( n + e ) O(n + e) O ( n + e ) O ( n + e ) O(n + e) O ( n + e )
适用于稀疏图
1 2 3 4 5 6 7 8 9 10 void add (int u, int v) nxt[++cnt] = head[u]; to[cnt] = v; head[u] = cnt; } for (int i = head[u]; i; i = nxt[i]) { int v = to[i]; }
图的遍历
广度优先搜索
Breadth-First Search
依次访问当前节点,再依次访问它们所有尚未访问的邻接顶点,如此反复
以上策略和过程等同于树的 层次遍历
BFS 会构造出原图的一棵支撑树
实现
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 template <typename Tv, typename Te> void Graph<Tv, Te>::BFS (Rank v, Rank &dClock) { Queue<Rank> Q; status (v) = DISCOVERED; Q.enqueue (v); dTime (v) = dClock++; for (Rank fClock = 0 ; !Q.empty (); ) { if (dTime (v) < dTime (Q.front ())) dClock++, fClock = 0 ; v = Q.dequeue (); for (Rank u = firstNbr (v); u != -1 ; u = nextNbr (v, u)) { if (status (u) == UNDISCOVERED) { status (u) = DISCOVERED; Q.enqueue (u); dTime (u) = dClock; type (v, u) = TREE; parent (u) = v; } else { type (v, u) = CROSS; } } status (v) = VISITED; fTime (v) = fClock++; } }
性质及规律
经 BFS 后,所有边将确定方向,且被分为两类
BFS(v) 以 v v v bfs(s) 生成一个 BFS 森林,包含 c c c n − c n - c n − c e − n + c e - n + c e − n + c 无向图中,顶点 v v v u u u d i s t ( v , u ) dist(v, u) d i s t ( v , u )
BFS 过程中,队列 Q Q Q
其中的顶点按 d i s t ( s ) dist(s) d i s t ( s )
相邻顶点的 d i s t ( s ) dist(s) d i s t ( s )
首、末顶点的 d i s t ( s ) dist(s) d i s t ( s )
由树边联接的顶点,d i s t ( s ) dist(s) d i s t ( s )
由跨边联接的顶点,d i s t ( s ) dist(s) d i s t ( s ) 至多 相差 1
BFS 树中从 s s s v v v
深度优先搜索
Depth-First Search
DFS(s)
访问顶点 s s s
若 s s s u u u DFS(u)
否则,返回
对树而言,等效于 先序遍历
DFS 会构造出原图的一棵支撑树
实现
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 template <typename Tv, typename Te> void Graph<Tv, Te>::DFS (Rank v, Rank &clock) { dTime (v) = ++clock; status (v) = DISCOVERED; for (Rank u = firstNbr (v); u != -1 ; u = nextNbr (v, u)) { switch (status (u)) { case UNDISCOVERED: type (v, u) = TREE; parent (u) = v; DFS (u, clock); break ; case DISCOVERED: type (v, u) = BACKWARD; break ; default : type (v, u) = dTime (v) < dTime (u) ? FORWARD : CROSS; break ; } } status (v) = VISITED; fTime (v) = ++clock; }
与 bfs(s) 类似,dfs(s) 也可在 O ( n + e ) O(n + e) O ( n + e )
对于每一连通/可达分量,从其起始顶点 v v v DFS(v) 恰好 1 次
最终生成一个 DFS 森林(包含 c c c n − c n - c n − c
性质
活跃期 a c t i v e [ u ] = ( d T i m e [ u ] , f T i m e [ u ] ) active[u] = (dTime[u], fTime[u]) a c t i v e [ u ] = ( d T i m e [ u ] , f T i m e [ u ] )
括号引理:给定有向图 G = ( V , E ) G = (V, E) G = ( V , E )
u u u v v v ⟺ a c t i v e [ u ] ⊆ a c t i v e [ v ] \iff active[u] \subseteq active[v] ⟺ a c t i v e [ u ] ⊆ a c t i v e [ v ] u u u v v v ⟺ a c t i v e [ u ] ⊇ a c t i v e [ v ] \iff active[u] \supseteq active[v] ⟺ a c t i v e [ u ] ⊇ a c t i v e [ v ] u u u v v v ⟺ a c t i v e [ u ] ∩ a c t i v e [ v ] = ∅ \iff active[u] \cap active[v] = \varnothing ⟺ a c t i v e [ u ] ∩ a c t i v e [ v ] = ∅
边分类
T R E E ( v , u ) TREE(v, u) T R E E ( v , u )
可以从当前 v v v UNDISCOVERED 状态的 u u u
B A C K W A R D ( v , u ) BACKWARD(v, u) B A C K W A R D ( v , u )
试图从当前 v v v DISCOVERED 状态的 u u u
DFS 发现后向边 ⟺ \iff ⟺
F O R W A R D ( v , u ) FORWARD(v, u) F O R W A R D ( v , u )
试图从当前 v v v VISITED 状态的 u u u v v v 更早 被发现
C R O S S ( v , u ) CROSS(v, u) C R O S S ( v , u )
试图从当前 v v v VISITED 状态的 u u u u u u 更早 被发现
拓扑排序
双连通分量
无向图 的关节点:其删除之后,原图连通分量增多
无关节点的图,称作双连通图
极大的双连通子图,称作双连通分量
DFS 树中的叶节点,不可能是关节点
Highest Connected Ancestor,hca(v) 表示 s u b t r e e ( v ) subtree(v) s u b t r e e ( v ) 后向边 能抵达的最高祖先
由括号引理,dTime 越小的祖先,辈份越高
DFS 过程中,一旦发现后向边 ( v , u ) (v, u) ( v , u )
即取 hca(v) = min(hca(v), dTime(u))
DFS(u) 完成并返回 v v v
若有 hca(u) < dTime(v) ,则取 hca(v) = min(hca(u), hca(v))
否则可以断定,v v v { v } + s u b t r e e ( u ) \{v\} + subtree(u) { v } + s u b t r e e ( u )
实现
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 template <typename Tv, typename Te> void Graph<Tv, Te>::BCC (Rank v, int &clock, Stack<Rank> &S) { hca (v) = dTime (v) = ++clock; status (v) = DISCOVERED; S.push (v); for (Rank u = firstNbr (v); u != -1 ; u = nextNbr (v, u)) { switch (status (u)) { case UNDISCOVERED: parent (u) = v; type (v, u) = TREE; BCC (u, clock, S); if (hca (u) < dTime (v)) { hca (v) = min (hca (v), hca (u)); } else { while (u != S.pop ()); } break ; case DISCOVERED: type (v, u) = BACKWARD; if (u != parent (v)) hca (v) = min (hca (v), dTime (u)); break ; default ; break ; } } status (v) = VISITED; }
强联通分量
有向图 的强连通性:图中任意两个节点 u u u v v v u u u v v v v v v u u u
满足这种性质的图,称作强连通图
极大的强连通子图,称作强连通分量(SCC)
Lowest Reachable Ancestor,low(v) 表示从 s u b t r e e ( v ) subtree(v) s u b t r e e ( v ) 最多一条非树边 能抵达的、仍在栈中 的最早被发现的祖先
DFS 过程中,一旦发现一条非树边 ( v , u ) (v, u) ( v , u ) u u u
即取 low(v) = min(low(v), dTime(u))
DFS(u) 完成并返回 v v v
取 low(v) = min(low(v), low(u))(子节点能到达的最低点,父节点也能到)
若返回后发现 low(v) == dTime(v),则可以断定,v v v
此时,从栈顶到 v v v
实现
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 template <typename Tv, typename Te> void Graph<Tv, Te>::SCC (Rank v, int &clock, Stack<Rank> &S) { low (v) = dTime (v) = ++clock; status (v) = DISCOVERED; S.push (v); for (Rank u = firstNbr (v); u != -1 ; u = nextNbr (v, u)) { switch (status (u)) { case UNDISCOVERED: parent (u) = v; SCC (u, clock, S); low (v) = min (low (v), low (u)); break ; case DISCOVERED: low (v) = min (low (v), dTime (u)); break ; default : break ; } } if (low (v) == dTime (v)) { while (v != S.pop ()); } status (v) = VISITED; }
优先级搜索
不同的遍历算法,取决于顶点的 访问策略
可以为每个顶点 v v v priority(v)
每个顶点都有初始优先级数;并可能随算法的推进而调整
优先级数越大/小,优先级越低/高
统一框架
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 template <typename Tv, typename Te>template <typename PU> void Graph<Tv, Te>::PFS (Rank v, PU prioUpdater) { priority (v) = 0 ; status (v) = VISITED; while (1 ) { for (Rank k = 1 ; k < n; k++) { for (Rank u = firstNbr (v); u != - 1 ; u = nextNbr (v, u)) { prioUpdater (this , v, u); } int shortest = INT_MAX; for (Rank u = 0 ; u < n; u++) { if (status (u) == UNDISCOVERED && shortest > priority (u)) { shortest = priority (u); v = u; } } status (v) = VISITED; type (parent (v), v) = TREE; } } }
复杂度
考查内循环
更新,邻接矩阵 O ( n 2 ) O(n^2) O ( n 2 ) O ( n + e ) O(n + e) O ( n + e )
择优,每次 O ( n ) O(n) O ( n ) O ( n 2 ) O(n^2) O ( n 2 )
合计 O ( n 2 ) O(n^2) O ( n 2 )
采用优先级队列,可分别改至 O ( e ⋅ log e ) O(e \cdot \log e) O ( e ⋅ log e ) O ( n ⋅ log e ) O(n \cdot \log e) O ( n ⋅ log e )
合计 O ( ( n + e ) ⋅ log e ) O((n + e) \cdot \log e) O ( ( n + e ) ⋅ log e )
对于 稠密图 而言,反而是倒退
Dijkstra 算法
问题分类
SSSP:Single Source Shortest Path
给定顶点 s s s
APSP:All Pairs Shortest Path
找出每对顶点 u u u v v v
最短路径树
任一最短路径的前缀,也是一条最短路径
u ∈ π ( v ) o n l y i f π ( u ) ⊆ π ( v ) u \in \pi(v) \quad {\rm only\,\,if} \,\,\, \pi(u) \subseteq \pi(v) u ∈ π ( v ) o n l y i f π ( u ) ⊆ π ( v )
消除歧义:各边权重均为正,否则
Shortest Path Tree
所有最短路径的并,既 连通 也 无环
T = T n − 1 = ⋃ 0 ≤ i < n π ( u i ) \begin{aligned}T = T_{n - 1} = \bigcup_{0 \le i < n} \pi(u_i)\end{aligned} T = T n − 1 = 0 ≤ i < n ⋃ π ( u i )
算法与实现
∀ v ∉ V k , l e t p r i o r i t y ( v ) = ∥ s , v ∥ ≤ ∞ \forall v \not\in V_k, \,\, {\rm let} \, priority(v) = \lVert s, v \rVert \le \infty ∀ v ∈ V k , l e t p r i o r i t y ( v ) = ∥ s , v ∥ ≤ ∞ 套用 PFS 框架,为将 T k T_k T k T k + 1 T_{k + 1} T k + 1
选出优先级最高的跨边 e k e_k e k v k v_k v k 加入 T k T_k T k
随后更新 V ∖ V k + 1 V \setminus V_{k + 1} V ∖ V k + 1
只需枚举 v k v_k v k
p r i o r i t y ( u ) = min ( p r i o r i t y ( u ) , p r i o r i t y ( v k ) + ∥ v k , u ∥ ) {\rm priority}(u) = \min({\rm priority}(u), {\rm priority}(v_k) + \lVert v_k, u \rVert) p r i o r i t y ( u ) = min ( p r i o r i t y ( u ) , p r i o r i t y ( v k ) + ∥ v k , u ∥ )
1 2 3 4 5 6 7 8 9 10 11 g->pfs (0 , DijkPU <char , Rank>()); template <typename Tv, typename Te> struct DijkPU { virtual void operator () (Graph<Tv, Te>* g, Rank v, Rank u) if (g->status (u) != UNDISCOVERED) return ; if (g->priority (u) > g->priority (v) + g->weight (v, u)) { g->priority (u) = g->priority (v) + g->weight (v, u); g->parent (u) = v; } } }
Prim 算法
最小支撑树
总权重 w ( T ) = ∑ e ∈ F w ( e ) {\rm w}(T) = \sum_{e \in F} {\rm w}(e) w ( T ) = ∑ e ∈ F w ( e )
M S T ≠ S P T MST \ne SPT M S T = S P T 允许权值为负
支撑树所含边数相等,故可统一调整 increase(1 - findMin())
Cayley 公式:完全图 K n \mathcal{K}_n K n n n − 2 n^{n - 2} n n − 2
割与极短跨边
算法实现
∀ v ∉ V k , l e t p r i o r i t y ( v ) = ∥ V k , v ∥ ≤ ∞ \forall v \not\in V_k, \,\, {\rm let} \, priority(v) = \lVert V_k, v \rVert \le \infty ∀ v ∈ V k , l e t p r i o r i t y ( v ) = ∥ V k , v ∥ ≤ ∞ 枚举 v k v_k v k u u u p r i o r i t y ( u ) = min ( p r i o r i t y ( u ) , ∥ v k , u ∥ ) {\rm priority}(u) = \min({\rm priority}(u), \lVert v_k, u \rVert) p r i o r i t y ( u ) = min ( p r i o r i t y ( u ) , ∥ v k , u ∥ )
1 2 3 4 5 6 7 8 9 10 g->pfs (0 , PrimPU <char , Rank>()); template <typename Tv, typename Te> struct PrimPU { virtual void operator () (Graph<Tv, Te>* g, Rank v, Rank u) if (g->status (u) != UNDISCOVERED) return ; if (g->priority (u) > g->weight (v, u)) { g->priority (u) = g->weight (v, u); g->parent (u) = v; } } }
Kruskal 算法
贪心
根据代价,从小到大依次尝试各边
只要“安全”(不会形成环),就加入该边
正确性
Kruskal 引入的每条边都属于某棵 MST
也可归纳证明:任何时刻,算法选择的边集总是某棵 MST 的子图
并查集
给定一组互不相交的 等价类 ,各由其中一个成员作为代表
Find(x) :找到元素 x x x Union(x, y) :合并 x x x y y y
优化:路径压缩,启发式合并
Floyd 算法
给定带权网络 G G G
Floyd-Warshall
最短路径矩阵
时间 O ( n 3 ) O(n^3) O ( n 3 )
定义 d k ( u , v ) d^k(u, v) d k ( u , v ) k k k u u u v v v
d 0 ( u , v ) = w ( u , v ) d^0(u, v) = w(u, v) d 0 ( u , v ) = w ( u , v ) d k ( u , v ) = min { d k − 1 ( u , v ) , d k − 1 ( u , x ) + d k − 1 ( x , v ) } d^k(u, v) = \min\{d^{k - 1}(u, v), d^{k - 1}(u, x) + d^{k - 1}(x, v) \} d k ( u , v ) = min { d k − 1 ( u , v ) , d k − 1 ( u , x ) + d k − 1 ( x , v ) }
1 2 3 4 for (int k = 0 ; k < n; k++) for (int u = 0 ; u < n; u++) for (int v = 0 ; v < n; v++) A[u][v] = min (A[u][v], A[u][k] + A[k][v]);
优先级队列
概述
1 2 3 4 5 template <typename T> struct PQ { virtual void insert (T) 0 ; virtual T delMax () 0 ; virtual T &getMax () 0 ; };
只需查找极值元,则不必维护所有元素之间的全序关系,偏序 足矣
完全二叉堆
插入删除
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 template <typename T> void PQ_ComplHeap<T>::insert (T e) { Vector<T>::insert (e); percolateUp (_elem, size - 1 ); } typename <typename T> Rank percolateUp (T *A, Rank i) while (i > 0 ) { Rank j = Parent (i); if (A[j] >= A[i]) break ; swap (A[i], A[j]); i = j; } return i; } template <typename T> T PQ_ComlHeap<T>::delMax () { T maxElem = _elem[0 ]; _elem[0 ] = _elem[--_size]; percolateDown (_elem, _size, 0 ); return maxElem; } template <typename T> Rank percolateDown (T *A, Rank n, Rank i) Rank j; while (i != (j = ProperParent (A, n, i))) swap (A[i], A[j]), i = j; return i; }
e e e O ( log n ) O(\log n) O ( log n )
平均情况为,插入 O ( 1 ) O(1) O ( 1 ) O ( log n ) O(\log n) O ( log n )
建堆
自上而下(或自下而上)的上滤
1 2 for (Rank i = 1 ; i < n; i++) percolateUp (i);
最坏情况每个节点所需成本线性正比于其深度,总计 O ( n log n ) O(n \log n) O ( n log n )
自下而上的下滤
1 2 for (Rank i = n / 2 - 1 ; i != -1 ; i--) percolateDown (i);
一些应用
Min-Max Heap
最小-最大堆是一个完全二叉堆,具有最小堆和最大堆的特征
树中偶数层级的节点都不大于其后代,奇数层级的节点都不小于其后代
因此根为 M i n {\rm Min} M i n M a x {\rm Max} M a x
可以在 O ( log n ) O(\log n) O ( log n )
对顶堆
由一个大根堆与一个小根堆组成
小根堆维护大值 即前 k k k k k k
查询第 k k k O ( 1 ) O(1) O ( 1 ) O ( log n ) O(\log n) O ( log n )
维护(核心思想是保持小根堆的元素数量)、插入元素、删除第 k k k k k k
堆排序
相当于用堆优化 选择排序
首先建堆,然后不断迭代
总时间 O ( n ) + n ⋅ O ( log n ) = O ( n log n ) O(n) + n \cdot O(\log n) = O(n \log n) O ( n ) + n ⋅ O ( log n ) = O ( n log n )
最好情况为 O ( n ) O(n) O ( n )
就地算法,但不稳定
1 2 3 4 5 6 7 template <typename T> void Vector<T>::heapSort (Rank lo, Rank hi) { T *A = _elem + lo; Rank n = hi - lo; heapify (A, n); while (--n > 0 ) { swap (A[0 ], A[n]); percolateDown (A, n, 0 ); } }
锦标赛树
胜者树
是完全二叉树,叶节点为各个元素,内部节点为孩子比较后的胜者
锦标赛排序
流程
构造胜者树
选取树根元素
沿根向下找到对应叶子,将其无效化(置为 ± ∞ \pm \infty ± ∞
从叶子处向上重新进行比较,直至根
不断重复
空间 O ( n ) O(n) O ( n ) O ( n + n ⋅ log n ) = O ( n log n ) O(n + n \cdot \log n) = O(n \log n) O ( n + n ⋅ log n ) = O ( n log n )
不完全选取
借助锦标赛树,从 n n n k k k k ≪ n k \ll n k ≪ n
初始化 O ( n ) O(n) O ( n ) n − 1 n - 1 n − 1
迭代 k k k O ( k log n ) O(k \log n) O ( k log n ) log n \log n log n
常系数相较小顶堆更优
败者树
在胜者树的重赛过程中,须 交替 访问沿途节点及其兄弟
败者树也是完全二叉树,但其存储内容和胜者树不同
内部节点,记录对应比赛的败者
增设根的“父节点”,记录冠军
初始化
将比赛的 败者 存入其父节点,胜者 则继续向上一层
根节点的父节点即是全局的冠军
更新迭代
返回叶子进行重赛,元素只需与其 父节点中存储的败者 进行比赛
胜者:继续向上,和更上层节点的败者进行比赛
败者:留在父节点中,替换原来的败者
更新效率更高,用额外的空间使每次信息查找的成本降至最低
应用场景:外部排序中的 k k k 归并 多个有序段)
多叉堆
PFS 中各节点可组织为优先级队列,总体运行时间 O ( n + ( n + e ) ⋅ log n ) = ( n + e ⋅ log n ) O(n + (n + e) \cdot \log n) = (n + e \cdot \log n) O ( n + ( n + e ) ⋅ log n ) = ( n + e ⋅ log n )
将二叉堆改为多叉堆,堆高降低至 log d n \log_d n log d n
上滤成本 降 至 log d n \log_d n log d n
下滤成本 增 (d > 4 d > 4 d > 4 d ⋅ log d n = d ln d ⋅ ln n d \cdot \log_d n = \frac{d}{\ln d} \cdot \ln n d ⋅ log d n = l n d d ⋅ ln n
如此,PFS 运行时间将为 n ⋅ d ⋅ log d n + e ⋅ l o g d n = ( n ⋅ d + e ) ⋅ log d n n \cdot d \cdot \log_d n + e \cdot log_d n = (n \cdot d + e) \cdot \log_d n n ⋅ d ⋅ log d n + e ⋅ l o g d n = ( n ⋅ d + e ) ⋅ log d n
取 d ≈ e / n + 2 d \approx e / n + 2 d ≈ e / n + 2 O ( e ⋅ log e / n + 2 n ) O(e \cdot \log_{e / n + 2} n) O ( e ⋅ log e / n + 2 n )
稀疏图保持高效,稠密图改进极大
左式堆
堆合并
方法一:A.insert(B.delMax()) ,O ( m log ( n + m ) ) O(m \log (n + m)) O ( m log ( n + m ) )
方法二:union(A, B).heapify(n + m) ,O ( n + m ) O(n + m) O ( n + m )
两堆合并 = 二路归并
统一沿右侧藤,则所需时间 ∝ \propto ∝
若能控制藤长,则可 持续 高效合并
控制藤长
保持 堆序性 ,在堆合并过程中,只涉及少量节点 O ( log n ) O(\log n) O ( log n )
新条件 = 单侧倾斜
不能保证结构性,但这并非堆结构本质要求
Null Path Length,空节点路径长度
引入外部节点,转为真二叉树
n p l ( N U L L ) = 0 npl({\rm NULL}) = 0 n p l ( N U L L ) = 0 n p l ( x ) = 1 + min { n p l ( l c ( x ) ) , n p l ( r c ( x ) ) } npl(x) = 1 + \min\{npl({\rm lc}(x)), npl({\rm rc}(x))\} n p l ( x ) = 1 + min { n p l ( l c ( x ) ) , n p l ( r c ( x ) ) } $npl(x) = $ x x x 最近 距离 = 以 x x x 满子树 的高度
左式堆 ⇔ \Leftrightarrow ⇔
对任何内部节点 x x x n p l ( l c ( x ) ) ≥ n p l ( r c ( x ) ) npl({\rm lc}(x)) \ge npl({\rm rc}(x)) n p l ( l c ( x ) ) ≥ n p l ( r c ( x ) )
n p l ( x ) = 1 + n p l ( r c ( x ) ) npl(x) = 1 + npl({\rm rc}(x)) n p l ( x ) = 1 + n p l ( r c ( x ) ) 并不意味着左孩子高度不小于右孩子
左倾性不会影响堆序性
倾向于将更多节点分布于左侧分支
右侧链 rChain(x) :从节点 x x x
n p l ( r ) ≡ ∣ r C h a i n ( r ) ∣ = d npl(r) \equiv \left\vert rChain(r) \right\vert = d n p l ( r ) ≡ ∣ r C h a i n ( r ) ∣ = d 右侧链长为 d d d
2 d − 1 2^d - 1 2 d − 1 2 d + 1 − 1 2^{d + 1} - 1 2 d + 1 − 1
包含 n n n d ≤ ⌊ log 2 ( n + 1 ) ⌋ + 1 = O ( log n ) d \le \lfloor \log_2 (n + 1) \rfloor + 1 = O(\log n) d ≤ ⌊ log 2 ( n + 1 ) ⌋ + 1 = O ( log n )
合并算法
递归:前处理+后处理
合并之前,比较 priority 判断是否要交换节点
回溯之后,比较 NPL 比较是否要交换子堆
递归实现
1 2 3 4 5 6 7 8 9 template <typename T> BinNodePosi<T> merge (BinNodePosi<T> a, BinNodePosi<T> b) if (!a) return b; if (!b) return a; if (*a < *b) swap (a, b); (a->rc = merge (a->rc, b))->parent = a; if (!a->lc || (a->lc->npl < a->rc->npl)) swap (a->lc, a->rc); a->npl = a->rc ? 1 + a->rc->npl : 1 ; return a; }
迭代实现
1 2 3 4 5 6 7 8 9 10 11 12 13 14 template <typename T> BinNodePosi<T> merge (BinNodePosi<T> a, BinNodePosi<T> b) if (!a) return b; if (!b) return a; if (*a < *b) swap (a, b); for (; a->rc; a = a->rc) if (*(a->rc) < *b) b->parent = a; swap (a->rc, b); (a->rc = b)->parent = a; for (; a; b = a, a = a->parent) { if (!a->lc || (a->lc->npl < a->rc->npl)) swap (a->lc, a->rc); a->npl = a->rc ? a->rc->npl + 1 : 1 ; } return b; }
插入和删除
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 template <typename T> void PQ_LeftHeap<T>::insert (T e) { _root = merge (_root, new BinNode <T>(e, NULL )); _size++; } template <typename T> T PQ_LeftHeap<T>::delMax () { BinNodePosi<T> lHeap = _root->lc; if (lHeap) lHeap->parent = null; BinNodePosi<T> rHeap = _root->rc; if (rHeap) rHeap->parent = null; T e = _root->data; delete _root; _size--; _root = merge (lHeap, rHeap); return e; }
串
模式匹配
循模式访问
r a n d o m T + s u b t r i n g P {\rm random}\,\, T \, + \, {\rm subtring} \,\, P r a n d o m T + s u b t r i n g P n = ∣ T ∣ m = ∣ P ∣ n = \left\vert T \right\vert \quad m = \left\vert P \right\vert n = ∣ T ∣ m = ∣ P ∣ $ 2 \ll m \ll n$
蛮力策略
(最差情况下)最好复杂度:Ω ( n ) \Omega(n) Ω ( n ) P = s u f f i x ( T ) P = {\rm suffix}(T) P = s u f f i x ( T )
平均:O ( n ) O(n) O ( n )
最差:O ( n ⋅ m ) O(n \cdot m) O ( n ⋅ m )
1 2 3 4 5 6 7 8 9 int match (char *P, char *T) int n = strlen (T), i = 0 ; int m = strlen (P), j = 0 ; while (j < m && i < n) { if (T[i] == P[j]) { i++; j++; } else { i -= j - 1 ; j = 0 ; } } return i - j; }
KMP 算法
在任一时刻,都有 T[i - j, i) == P[0, j)
亦即已掌握了 T[i - j, i) 的所有信息,一旦失败,就应已知哪些位置 值得/不必 对齐
T[i - j', i) 可径直接受,则不必再做比对如此,i i i 不必回退
比对成功,则与 j j j
否则,j j j j ′ j' j ′ 继续比对
1 2 3 4 5 6 7 8 9 10 11 int match (char *P, char *T) int *next = buildNext (P); int n = strlen (T), i = 0 ; int m = strlen (P), j = 0 ; while (j < m && i < n) { if (j < 0 || T[i] == P[j]) { i++; j++; } else j = next[j]; } delete [] next; return i - j; }
next [] 表
最长自匹配:快速右移 + 绝不回退
∀ j ≥ 1 , N ( P , j ) = { 0 ≤ t < j ∣ P [ 0 , t ) = P [ j − t , j ) } \forall j \ge 1, \, {\rm N}(P, j) = \{0 \le t < j \,\, | \,\, P[0,t) = P[j - t, j)\} ∀ j ≥ 1 , N ( P , j ) = { 0 ≤ t < j ∣ P [ 0 , t ) = P [ j − t , j ) } n e x t [ j ] = max { N ( P , j ) } {\rm next}[j] = \max\{N(P, j)\} n e x t [ j ] = max { N ( P , j ) } ⇔ \Leftrightarrow ⇔ P [ 0 , j ) P[0, j) P [ 0 , j ) 真前后缀 的长度
传递链
n e x t k + 1 [ j ] = n e x t [ n e x t k [ j ] ] {\rm next}^{k + 1}[j] = {\rm next}[{\rm next}^k[j]] n e x t k + 1 [ j ] = n e x t [ n e x t k [ j ] ] ∀ j ≥ 1 , N ( P , j ) = { 0 , … , n e x t 2 [ j ] , n e x t 1 [ j ] } \forall j \ge 1, \, {\rm N}(P, j) = \{ 0, \dots, {\rm next}^2[j], {\rm next}^1[j] \} ∀ j ≥ 1 , N ( P , j ) = { 0 , … , n e x t 2 [ j ] , n e x t 1 [ j ] } − 1 ← 0 ⋯ ← n e x t 2 [ j ] ← n e x t 1 [ j ] ← n e x t 0 [ j ] = j -1 \leftarrow 0 \dots \leftarrow {\rm next}^2[j] \leftarrow {\rm next}^1[j] \leftarrow {\rm next}^0[j] = j − 1 ← 0 ⋯ ← n e x t 2 [ j ] ← n e x t 1 [ j ] ← n e x t 0 [ j ] = j
减而治之
P P P j + 1 j + 1 j + 1 j j j 一个 字符n e x t [ j + 1 ] = n e x t [ j ] + 1 ⟺ P [ j ] = P [ n e x t [ j ] ] {\rm next}[j + 1] = {\rm next}[j] + 1 \iff P[j] = P[{\rm next}[j]] n e x t [ j + 1 ] = n e x t [ j ] + 1 ⟺ P [ j ] = P [ n e x t [ j ] ] n e x t [ 0 ] = − 1 , n e x t [ 1 ] = 0 {\rm next}[0] = -1, \,\, {\rm next}[1] = 0 n e x t [ 0 ] = − 1 , n e x t [ 1 ] = 0
1 2 3 4 5 6 7 8 9 10 11 12 int *buildNext (char *P) int m = strlen (P), j = 0 ; int *next = new int [m]; int t = next[0 ] = -1 ; while (j < m - 1 ) { if (t < 0 || P[t] == P[j]) { ++t; ++j; next[j] = t; } else t = next[j]; } return next; }
分析
摊还分析
1 2 3 4 while (j < m && i < n) if (j < 0 || T[i] == P[j]) i++, j++; else j = next[j];
计步器 k 随着迭代单调递增,且 k ≤ 2 n − 1 k \le 2n - 1 k ≤ 2 n − 1
故 build 和 match 总时间复杂度为 O ( n + m ) O(n + m) O ( n + m )
每一个 P 串,相当于一台 自动机
适用于顺序存储介质
单次匹配概率越大,优势越明显
再改进
经验 ∼ \sim ∼ T[i - j, i) 是什么
教训 ∼ \sim ∼ T[i] 不是什么
- 进一步避免 **注定错误** 的比较
- $\forall j \ge 1, \, {\rm N}(P, j) = \{0 \le t < j \,\, | \,\, P[0,t) = P[j - t, j) \cap {\color{Red}{P[t] \ne P[j]}}\} \cup \{{\color{Red}{-1}}\}$
- ${\color{Red}{-1}} \in {\rm N}(P, j) \ne \varnothing$, ${\rm next}[j] = \max\{{\rm N}(P, j)\}$
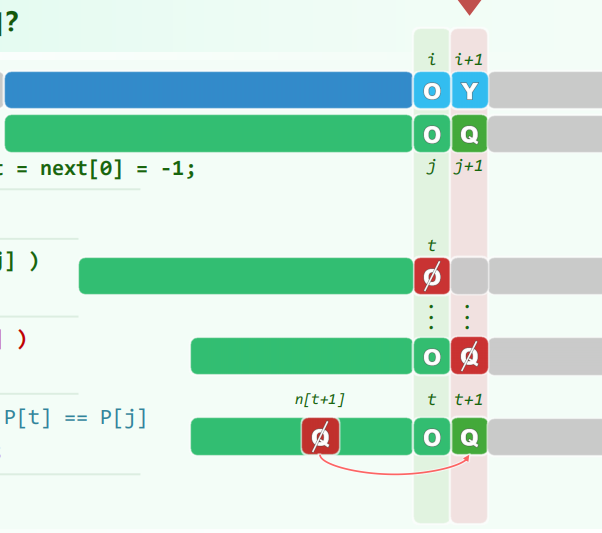
1 2 3 4 5 6 7 8 9 10 11 12 13 14 int *buildNext (char *P) int m = strlen (P), j = 0 ; int *next = new int [m]; int t = next[0 ] = -1 ; while (j < m - 1 ) { if (t >= 0 && P[t] != P[j]) { t = next[t]; } else if (P[++t] != P[++j]) { next[j] = t; } else { next[j] = next[t]; } } return next; }
BM 算法
通过 后缀匹配 获得比前缀匹配更多的信息来实现更快的字符跳转
迭代: 自右向左 依次比对,找到极大的匹配后缀
若完全匹配,则可返回
否则查表(类似于 next[] 的作用)确定 P 右移 的适当位置,重新 自右向左比对
1 2 3 4 5 6 7 8 9 10 11 int match (char *T, char *P) int *bc = buildBC (P); int *gs = buildGS (P); int n = strlen (T), i = 0 ; int m = strlen (P), j = 0 ; for (i = 0 ; i + m < n; i += max (gs[j], j - bc[T[i + j]])) { for (j = m - 1 ; j >= 0 && P[j] == T[i + j]); j--); if (j < 0 ) break ; } delete [] bc; return i; }
BC 策略
bc [] 表
1 2 3 4 5 6 7 int *buildBC (char *P) int *bc = new int [256 ]; for (size_t j = 0 ; j < 256 ; j++) bc[j] = -1 ; for (size_t m = strlen (P), j = 0 ; j < m; j++) bc[P[j]] = j; return bc; }
不倾向于使用二维的 bc[][] 表
若其能发挥作用,则此时的好后缀必然很长——同时使用的 gs[] 表完全可以替代
分析
最好情况:O ( n / m ) O(n / m) O ( n / m )
只要 P 不含 T[i + j] ,则可直接移动 m m m
单次匹配概率越小,性能优势越明显
最差情况:O ( n × m ) O(n \times m) O ( n × m )
每轮迭代,都要在扫过整个 P 之后,方能确定右移 一个 字符
单次匹配概率越大的场合,性能越接近于蛮力算法
bc[] 表仅仅利用了 失配 比对提供的信息(教训)
GS 策略
Good-Suffix Shift,扫描比对中断于 T [ i + j ] = X ≠ O = P [ j ] T[i + j] = X \ne O = P[j] T [ i + j ] = X = O = P [ j ] U = P ( j , m ) U = P(j, m) U = P ( j , m )
下一对齐位置 必须使得
U U U V ( k ) = P ( k , k + m − j ) V(k) = P(k, k + m - j) V ( k ) = P ( k , k + m − j ) P [ k ] ≠ O = P [ j ] P[k] \ne O = P[j] P [ k ] = O = P [ j ]
完全匹配
若存在这样的子串 V ( k ) V(k) V ( k ) 靠后者 ,通过右移使之与 U U U
部分匹配
若不存在,则所有的前缀 P [ 0 , t ) P[0, t) P [ 0 , t ) U U U 后缀 匹配的最长者(以免错过可能的成功比对)
t t t P P P m + i m + i m + i
gs [] 表
∀ 0 ≤ j < m , s s [ j ] = max { 0 ≤ s ≤ j + 1 ∣ P ( j − s , j ] = P [ m − s , m ) } \forall \, 0 \le j < m, ss[j] = \max\{ 0 \le s \le j + 1 \,\, | \,\, P(j - s, j] = P[m - s, m) \} ∀ 0 ≤ j < m , s s [ j ] = max { 0 ≤ s ≤ j + 1 ∣ P ( j − s , j ] = P [ m − s , m ) }
M S [ j ] = P ( j − s s [ j ] , j ] MS[j] = P(j - ss[j], j] M S [ j ] = P ( j − s s [ j ] , j ] P [ 0 , j ] P[0, j] P [ 0 , j ] 最长者
s s [ ] ⇒ g s [ ] ss[] \Rightarrow gs[] s s [ ] ⇒ g s [ ]
若 s s [ j ] = j + 1 ss[j] = j + 1 s s [ j ] = j + 1 i < m − j − 1 i < m - j - 1 i < m − j − 1 m − j − 1 m - j - 1 m − j − 1 g s [ i ] gs[i] g s [ i ]
若 s s [ j ] ≤ j ss[j] \le j s s [ j ] ≤ j m − j − 1 m - j - 1 m − j − 1 g s [ m − s s [ j ] − 1 ] gs[m - ss[j] - 1] g s [ m − s s [ j ] − 1 ]
s s [ ] ss[] s s [ ]
自后向前逆向扫描,使用双指针维护一个 “已知匹配框”
P ( l o , h i ] P(lo, hi] P ( l o , h i ]
由于 j 严格单调递减、lo 严格单调非增,且每次迭代两者之一会减少,故总时间复杂度为 O ( m ) O(m) O ( m )
本质上是 Z-Algorithm(求解最长公共前缀 LCP)在模式串 P P P
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 int *buildSS (char *P) int m = strlen (P); int *ss = new int [m]; ss[m - 1 ] = m; for (int lo = m - 1 , hi = m - 1 , j = lo - 1 ; j >= 0 ; j--) { if (lo < j && ss[m - 1 - (hi - j)] < j - lo) ss[j] = ss[m - 1 - (hi - j)]; else { hi = j; lo = min (lo, hi); while (lo >= 0 && P[lo] == P[m - 1 - (hi - lo)]) lo--; ss[j] = hi - lo; } } return ss; }
g s [ ] gs[] g s [ ]
核心是画家算法,按优先级低高先后处理 gs[] 的不同规则
其中的“双层循环”同样由于 i, j 两个指针单调变化,故总体是线性的,于是整个算法复杂度为 O ( m ) O(m) O ( m )
1 2 3 4 5 6 7 8 9 10 11 12 int *buildGS (char *P) int *ss = buildSS (P); int m = strlen (P); int *gs = new int [m]; for (int j = 0 ; j < m; j++) gs[j] = m; for (int i = 0 , j = m - 1 ; j >= 0 ; j--) if (j + 1 == ss[j]) while (i < m - j - 1 ) gs[i++] = m - j - 1 ; for (int j = 0 ; j < m - 1 ; j++) gs[m - ss[j] - 1 ] = m - j - 1 ; delete [] ss; return gs; }
性能分析
空间:∣ b c ∣ + ∣ g s ∣ = O ( ∣ Σ ∣ + m ) \left\vert bc \right\vert + \left\vert gs \right\vert = O(\left\vert \Sigma \right\vert + m) ∣ b c ∣ + ∣ g s ∣ = O ( ∣ Σ ∣ + m )
预处理:O ( ∣ Σ ∣ + m ) O(\left\vert \Sigma \right\vert + m) O ( ∣ Σ ∣ + m )
查找效率
最好 O ( n / m ) O(n / m) O ( n / m )
最差 O ( n + m ) O(n + m) O ( n + m )
影响因素:单词比对成功的概率
通常,Pr = 1 / s \Pr = 1 / s Pr = 1 / s
Karp-Rabin 算法
凡物皆数
Gödel Numbering
逻辑系统的符号、表达式、公式、命题、定理、公理等,均可表示为 自然数
每个 有限 维的自然数向量(包括字符串),都唯一对应于某个 自然数
⟨ a 1 , a 2 , … , a n ⟩ ⇔ p ( 1 ) 1 + a 1 × p ( 2 ) a 2 + 1 × ⋯ × p ( n ) a n + 1 \left\langle a_1, a_2, \dots, a_n \right\rangle \,\, \Leftrightarrow p(1)^{1 + a_1} \times p(2)^{a_2 + 1} \times \cdots \times p(n)^{a_n + 1} ⟨ a 1 , a 2 , … , a n ⟩ ⇔ p ( 1 ) 1 + a 1 × p ( 2 ) a 2 + 1 × ⋯ × p ( n ) a n + 1 p ( k ) p(k) p ( k ) k k k
Cantor Numbering
长度 有限 的字符串,都可视作 d = 1 + ∣ Σ ∣ d = 1 + \left\vert \Sigma \right\vert d = 1 + ∣ Σ ∣
长度 无限 的字符串,都可视作 [ 0 , 1 ) [0, 1) [ 0 , 1 ) d d d
串亦为数
每个字符串对应一个 d d d
P P P T T T 仅当 T T T P P P 如果 ∣ Σ ∣ \left\vert \Sigma \right\vert ∣ Σ ∣ O ( 1 ) O(1) O ( 1 )
散列压缩
字宽
可以在 O ( r = log n ) O(r = \log n) O ( r = log n ) p o w e r ( n ) = a n {\rm power}(n) = a^n p o w e r ( n ) = a n
a n a^n a n Θ ( n ) \Theta(n) Θ ( n ) 常数代价准则、对数代价准则
排序
快速排序
分而治之
pivot,轴点:max [ l o , m i ) ≤ [ m i ] ≤ min ( m i , h i ) \max[lo, mi) \le [mi] \le \min(mi, hi) max [ l o , m i ) ≤ [ m i ] ≤ min ( m i , h i ) 前缀、后缀各自(递归)排序之后,原序列自然有序
1 2 3 4 5 6 template <typename T> void Vector<T>::quickSort (Rank lo, Rank hi) { if (hi - lo < 2 ) return ; Rank mi = partition (lo, hi); quickSort (lo, mi); quickSort (mi + 1 , hi); }
划分后,轴点必然已经 就位
一个序列有序, 当且仅当 所有元素皆为轴点
快速排序,即为 将所有元素转化为轴点 的过程
快速划分:LUG
任取一个候选者
交替向内移动 lo 和 hi ,并逐个检查当前元素
lo == hi 时,将候选者嵌入 L、G 之中,即成轴点
1 2 3 4 5 6 7 8 9 10 11 template <typename T> Rank Vector<T>::partition (Rank lo, Rank hi) { swap (_elem[lo], _elem[lo + rand () % (hi - lo)]); T pivot = _elem[lo]; while (lo < hi) { do { hi--; } while (lo < hi && pivot <= _elem[hi]); if (lo < hi) _elem[lo] = _elem[hi]; do { lo++; } while (lo < hi && _elem[lo] <= pivot); if (lo < hi) _elem[hi] = _elem[lo]; } _elem[hi] = pivot; return hi; }
线性时间:lo 、hi 累计移动距离不超过 O ( n ) O(n) O ( n )
就地:只需 O ( 1 ) O(1) O ( 1 )
不稳定
空间复杂度
空间复杂度 ∼ \sim ∼
最好 O ( log n ) O(\log n) O ( log n ) O ( n ) O(n) O ( n ) O ( log n ) O(\log n) O ( log n )
迭代化+贪心
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 #define Put(K, s, t) { if (1 < (t) - (s)) { K.push(s); K.push(t); } } #define Get(K, s, t) { t = K.pop(); s = K.pop(); } template <typename T> void Vector<T>::quickSort (Rank lo, Rank hi) { Stack<Rank> Task; Put (Task, lo, hi); while (!Task.empty ()) { Get (Task, lo, hi); Rank mi = partition (lo, hi); if (mi - lo < hi - mi) { Put (Task, mi + 1 , hi); Put (Task, lo, mi); } else { Put (Task, lo, mi); Puts (Task, mi + 1 , hi); } } }
可归纳假设证得,所需空间不超过 O ( log n ) O(\log n) O ( log n )
如果采用 递归 方式对顺序表进行快速排序,递归次数和递归深度与每次划分后得到的分区的处理顺序 无关 (即每次先处理 较长或较短 的分区)
时间性能
最好:每次划分都(接近)平均
T ( n ) = 2 ⋅ T ( ( n − 1 ) / 2 ) + O ( n ) = O ( n log n ) T(n) = 2 \cdot T((n - 1) / 2) + O(n) = O(n \log n) T ( n ) = 2 ⋅ T ( ( n − 1 ) / 2 ) + O ( n ) = O ( n log n )
最坏:每次划分都极不均衡
T ( n ) = T ( n − 1 ) + T ( 0 ) + O ( n ) = O ( n 2 ) T(n) = T(n - 1) + T(0) + O(n) = O(n^2) T ( n ) = T ( n − 1 ) + T ( 0 ) + O ( n ) = O ( n 2 )
采用随机选取、三者取中之类的策略,只能降低最坏情况的概率
递归深度
好轴点:落在宽度为 λ ⋅ n \lambda \cdot n λ ⋅ n
递归深度(常规随机):
最坏情况 Ω ( n ) \Omega(n) Ω ( n )
平均情况递归 O ( log n ) O(\log n) O ( log n )
实际上,除非轴点过于侧偏,否则都会有效地缩短递归深度
断言
在任何一条递归路径上,好轴点不会多于 d ( n , λ ) = log 2 1 + λ n d(n, \lambda) = \log_{\frac{2}{1 + \lambda}}n d ( n , λ ) = log 1 + λ 2 n
抵达 1 λ ⋅ d ( n , λ ) \frac{1}{\lambda} \cdot d(n, \lambda) λ 1 ⋅ d ( n , λ ) 期望 地出现 d ( n , λ ) d(n, \lambda) d ( n , λ ) 之前 终止递归
以 λ = 0.5 \lambda = 0.5 λ = 0 . 5 极小 的概率超过 D ( n , 1 2 ) = 2 λ ⋅ d ( n , 1 2 ) ≈ 9.64 ⋅ log 2 n D(n, \frac{1}{2}) = \frac{2}{\lambda} \cdot d(n, \frac{1}{2}) \approx 9.64 \cdot \log_2 n D ( n , 2 1 ) = λ 2 ⋅ d ( n , 2 1 ) ≈ 9 . 6 4 ⋅ log 2 n
比较次数
递推分析
记期望比较次数为 T ( n ) T(n) T ( n ) T ( 1 ) = 0 T(1) = 0 T ( 1 ) = 0
T ( n ) = ( n − 1 ) + 1 n ⋅ ∑ k = 0 n − 1 [ T ( k ) + T ( n − k − 1 ) ] = ( n − 1 ) + 2 n ⋅ ∑ k = 0 n − 1 T ( k ) \begin{aligned} T(n) &= (n - 1) + \frac{1}{n} \cdot \sum_{k = 0}^{n - 1} [T(k) + T(n - k - 1)] \\ &= (n - 1) + \frac{2}{n} \cdot \sum_{k = 0}^{n - 1}T(k)\end{aligned} T ( n ) = ( n − 1 ) + n 1 ⋅ k = 0 ∑ n − 1 [ T ( k ) + T ( n − k − 1 ) ] = ( n − 1 ) + n 2 ⋅ k = 0 ∑ n − 1 T ( k ) n ⋅ T ( n ) − ( n + 1 ) ⋅ T ( n − 1 ) = 2 ⋅ ( n − 1 ) n \cdot T(n) - (n + 1) \cdot T(n - 1) = 2 \cdot (n - 1) n ⋅ T ( n ) − ( n + 1 ) ⋅ T ( n − 1 ) = 2 ⋅ ( n − 1 ) T ( n ) n + 1 = 4 ⋅ ∑ k − 2 n 1 k + 1 − 2 ⋅ ∑ k = 2 n 1 k = 2 ⋅ ∑ k = 1 n + 1 1 k + 2 n + 1 − 4 ≈ 2 ln n \begin{aligned} \frac{T(n)}{n + 1} = 4 \cdot \sum_{k - 2}^n \frac{1}{k + 1} - 2 \cdot \sum_{k = 2}^n \frac{1}{k} = 2 \cdot \sum_{k = 1}^{n + 1} \frac{1}{k} + \frac{2}{n + 1} - 4 \approx 2 \ln n\end{aligned} n + 1 T ( n ) = 4 ⋅ k − 2 ∑ n k + 1 1 − 2 ⋅ k = 2 ∑ n k 1 = 2 ⋅ k = 1 ∑ n + 1 k 1 + n + 1 2 − 4 ≈ 2 ln n T ( n ) ≈ 2 ⋅ n ⋅ ln n ≈ 1.386 ⋅ n log n T(n) \approx 2 \cdot n \cdot \ln n \approx 1.386 \cdot n \log n T ( n ) ≈ 2 ⋅ n ⋅ ln n ≈ 1 . 3 8 6 ⋅ n log n
后向分析
设 排序后 的序列为 { a 0 , a 1 , … , a i , … , a j , … , a n − 1 } \{a_0, a_1, \dots, a_i, \dots, a_j, \dots, a_{n - 1}\} { a 0 , a 1 , … , a i , … , a j , … , a n − 1 }
则期望的比较次数为 T ( n ) = ∑ i = 0 n − 2 ∑ j = i + 1 n − 1 Pr ( i , j ) = ∑ j = 1 n − 1 ∑ i = 0 j − 1 Pr ( i , j ) \begin{aligned}T(n) = \sum_{i = 0}^{n - 2}\sum_{j = i + 1}^{n - 1} \Pr(i, j) = \sum_{j = 1}^{n - 1}\sum_{i = 0}^{j - 1} \Pr(i, j) \end{aligned} T ( n ) = i = 0 ∑ n − 2 j = i + 1 ∑ n − 1 Pr ( i , j ) = j = 1 ∑ n − 1 i = 0 ∑ j − 1 Pr ( i , j )
即每一对 ⟨ a i , a j ⟩ \langle a_i, a_j \rangle ⟨ a i , a j ⟩
quickSort 的过程可以理解为:将所有元素转化为 pivot
⟨ a i , a j ⟩ \left\langle a_i, a_j \right\rangle ⟨ a i , a j ⟩ 当且仅当 在 { a i , a i + 1 , … , a j − 1 , a j } \{a_i, a_{i + 1}, \dots, a_{j - 1}, a_j\} { a i , a i + 1 , … , a j − 1 , a j } a i a_i a i a j a_j a j ⇒ \Rightarrow ⇒ Pr ( i , j ) = 2 j − i + 1 \Pr(i, j) = \frac{2}{j - i + 1} Pr ( i , j ) = j − i + 1 2 T ( n ) = ∑ j = 1 n − 1 ∑ d = 1 j 2 d + 1 ≈ ∑ j = 1 n − 1 2 ⋅ ( ln j − 1 ) ≤ 2 ⋅ n ⋅ ln n \begin{aligned}T(n) = \sum_{j = 1}^{n - 1}\sum_{d = 1}^{j} \frac{2}{d + 1} \approx \sum_{j = 1}^{n - 1} 2 \cdot (\ln j - 1) \le 2 \cdot n \cdot \ln n \end{aligned} T ( n ) = j = 1 ∑ n − 1 d = 1 ∑ j d + 1 2 ≈ j = 1 ∑ n − 1 2 ⋅ ( ln j − 1 ) ≤ 2 ⋅ n ⋅ ln n
快速划分:DUP
1 2 3 4 5 6 7 8 9 10 11 12 while (lo < hi) { do { hi--; } while (lo < hi && pivot < _elem[hi]); do { lo++; } while (lo < hi && _elem[lo] < pivot); }
遇到连续的相等元素时
lo 和 hi 会交替移动使得切分点接近于 l o + h i 2 \frac{lo + hi}{2} 2 l o + h i
交换操作有所增加,更不稳定
快速划分:LGU
S = [ l o , h i ) = [ l o ] + ( l o , m i ] + ( m i , k ) + [ k , h i ) = p i v o t + L + G + U S = [lo, hi) = [lo] + (lo, mi] + (mi, k) + [k, hi) = pivot + L + G + U S = [ l o , h i ) = [ l o ] + ( l o , m i ] + ( m i , k ) + [ k , h i ) = p i v o t + L + G + U
1 2 3 4 5 6 7 8 9 template <typename T> Rank Vector<T>::partition (Rank lo, Rank hi) { swap (_elem[lo], _elem[lo + rand () % (hi - lo)]); T pivot = _elem[lo]; Rank mi = lo; for (Rank k = lo + 1 ; k < hi; k++) if (_elem[k] < pivot) swap (_elem[++mi], _elem[k]); swap (_elem[mi], _elem[lo]); return mi; }
选取
k-selection :在任意一组可比较大小的元素中,找出其对应非降排序序列 S S S S [ k ] S[k] S [ k ]
众数
无序向量中,若有 一半以上 元素同为 m m m
必要性:众数若存在,则其必是中位数
时间 O ( n ) O(n) O ( n ) O ( 1 ) O(1) O ( 1 )
若在向量 A A A P P P x x x 恰 占半数,则 A A A A − P A - P A − P m m m m m m A A A
若 x = m x = m x = m P P P m m m 保持不变
若 x ≠ m x \ne m x = m P P P m m m 不致缩小
若将众数的标准从“一半以上”改作“至少一半”
则可以按照以上思路循环两次,以避免算法最后返回了一个错误的候选
或一开始选择一个数验证、若不是则剪除该元素再执行算法(控制元素总数为奇数)
1 2 3 4 5 6 7 8 9 10 11 template <typename T> T majCandidate (Vector<T> A) T maj; for (Rank c = 0 , i = 0 ; i < A.size (); i++) { if (c == 0 ) { maj = A[i]; c = 1 ; } else { maj == A[i] ? c++ : c--; } } return maj; }
中位数
蛮力
排序+遍历,O ( n log n ) + O ( k ) = O ( n log n ) O(n \log n) + O(k) = O(n \log n) O ( n log n ) + O ( k ) = O ( n log n )
堆
将所有元素组织为小顶堆,连续调用 delMin()
O ( n ) + O ( k log n ) O(n) + O(k \log n) O ( n ) + O ( k log n )
任选 k + 1 k + 1 k + 1 insert 并 delMax()
O ( k ) + O ( n log k ) O(k) + O(n \log k) O ( k ) + O ( n log k )
将输入任意划分组织为 k k k n − k n -k n − k
O ( n ) + O ( min ( k , n − k ) log n ) O(n) + O(\min(k, n - k) \log n) O ( n ) + O ( min ( k , n − k ) log n )
下界:Ω ( n ) \Omega(n) Ω ( n )
QuickSelect
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 template <typename T> Rank quickSelect (T const *A, Rank n, Rank k) Vector<Rank> R (n) ; for (Rank k = 0 ; k < n; k++) R.insert (k); for (Rank lo = 0 , hi = n; ; ) { swap (R[lo], R[lo + rand () % (hi - lo)]); T pivot = A[R[lo]]; Rank mi = lo; for (Rank i = lo + 1 ; i < hi; i++) { if (A[R[i]] < pivot) swap (R[++mi], R[i]); } swap (R[lo], R[mi]); if (mi < k) lo = mi + 1 ; else if (k < mi) hi = mi; else return R[mi]; } }
记期望比较次数为 T ( n ) T(n) T ( n ) T ( 1 ) = 0 T(1) = 0 T ( 1 ) = 0
T ( n ) = ( n − 1 ) + 1 n ⋅ ∑ k = 0 n − 1 max { T ( k ) , T ( n − k − 1 ) } ≤ ( n − 1 ) + 2 n ⋅ ∑ k = n / 2 n − 1 T ( k ) \begin{aligned} T(n) &= (n - 1) + \frac{1}{n} \cdot \sum_{k = 0}^{n - 1} \max\{T(k), T(n - k - 1)\} \\ &\le (n - 1) + \frac{2}{n} \cdot \sum_{k = n / 2}^{n - 1}T(k)\end{aligned} T ( n ) = ( n − 1 ) + n 1 ⋅ k = 0 ∑ n − 1 max { T ( k ) , T ( n − k − 1 ) } ≤ ( n − 1 ) + n 2 ⋅ k = n / 2 ∑ n − 1 T ( k ) T ( n ) < 4 ⋅ n → T ( n ) = O ( n ) T(n) < 4 \cdot n \rightarrow T(n) = O(n) T ( n ) < 4 ⋅ n → T ( n ) = O ( n )
T ( n ) ≤ ( n − 1 ) + 2 n ⋅ ∑ k = n / 2 n − 1 4 k ≤ ( n − 1 ) + 3 n < 4 n \begin{aligned} T(n) \le (n - 1) + \frac{2}{n} \cdot \sum_{k = n / 2}^{n - 1} 4k \le (n - 1) + 3n < 4n\end{aligned} T ( n ) ≤ ( n − 1 ) + n 2 ⋅ k = n / 2 ∑ n − 1 4 k ≤ ( n − 1 ) + 3 n < 4 n
LinearSelect
希尔排序
框架
ShellSort:将整个序列视作一个矩阵,逐列各自排序
递减增量
由粗到细,重排矩阵,使其更窄,再次逐列排序 h-sorting
如此往复,直至矩阵变为一列 1-sorting
步长序列:由各矩阵宽度 逆向 排列而成的序列
H = { h 1 = 1 , h 2 , … , h k , … } \mathcal{H} = \{h_1 = 1, h_2, \dots, h_k, \dots\} H = { h 1 = 1 , h 2 , … , h k , … } A [ k ] = B [ k / h ] [ k % h ] A[k] = B[k / h][k \% h] A [ k ] = B [ k / h ] [ k % h ]
正确性:最后一次迭代,等同于全排序
一个 g-ordered 序列在 h-sorted 之后仍保持 g-ordered
一个序列同时保持 g-ordered 和 h-ordered 称为 (g, h)-ordered ,此时对任意 m , n ∈ N + m, n \in N_+ m , n ∈ N + (mg + nh)-ordered
对任意互素 p , q ∈ N + p, q \in N_+ p , q ∈ N + (p, q)-ordered 序列中逆序对的间距不大于 ( p − 1 ) × ( q − 1 ) (p - 1) \times (q - 1) ( p − 1 ) × ( q − 1 )
1 2 3 4 5 6 7 8 9 template <typename T> void Vector<T>::shellSort (Rank lo, Rank hi) { for (Rank d = 0x7FFFFFF ; d > 0 ; d >>= 1 ) for (Rank j = lo + d; j < hi; j++) { T x = _elem[j]; Rank i = j; while (lo + d <= i && x < _elem[i - d]) _elem[i] = _elem[i - d], i -= d; _elem[i] = x; } }
最好情况 O ( n ) O(n) O ( n )
Shell 序列
Shell’s Sequence
H s h e l l = { 1 , 2 , 4 , 8 , … , 2 k , … } \mathcal{H}_{shell} = \{1, 2, 4, 8, \dots, 2^k, \dots\} H s h e l l = { 1 , 2 , 4 , 8 , … , 2 k , … } 最坏情况下 Ω ( n 2 ) \Omega(n^2) Ω ( n 2 )
考查子序列 A = u n s o r t e d [ 2 N − 1 , 2 N ) A = {\rm unsorted}[2^{N - 1}, 2^N) A = u n s o r t e d [ 2 N − 1 , 2 N ) B = u n s o r t e d [ 0 , 2 N − 1 ) B = {\rm unsorted}[0, 2^{N - 1}) B = u n s o r t e d [ 0 , 2 N − 1 )
进行 1-sorting 时仍有很多逆序对
根源在于,H s h e l l \mathcal{H}_{shell} H s h e l l
PS’s Sequence
H P S = H s h e l l − 1 = { 2 k − 1 ∣ k ∈ N } = { 1 , 3 , 7 , 15 , 31 , … } \mathcal{H}_{PS} = \mathcal{H}_{shell} - 1 = \{2^k - 1 \,\,|\,\, k \in N\} = \{1, 3, 7, 15, 31, \dots\} H P S = H s h e l l − 1 = { 2 k − 1 ∣ k ∈ N } = { 1 , 3 , 7 , 1 5 , 3 1 , … } 时间复杂度 O ( n 3 / 2 ) O(n^{3 / 2}) O ( n 3 / 2 )
平均为 O ( n 5 / 4 ) O(n^{5 / 4}) O ( n 5 / 4 )
Pratt’s Sequence
H p r a t t = { 2 p ⋅ 3 q ∣ p , q ∈ N } = { 1 , 2 , 3 , 4 , 6 , 8 , 9 , 12 , 16 , 18 , … } \mathcal{H}_{pratt} = \{2^p \cdot 3^q \,\, | \,\, p, q \in N\} = \{1, 2, 3, 4, 6, 8, 9, 12, 16, 18, \dots\} H p r a t t = { 2 p ⋅ 3 q ∣ p , q ∈ N } = { 1 , 2 , 3 , 4 , 6 , 8 , 9 , 1 2 , 1 6 , 1 8 , … } 时间复杂度 O ( n log 2 n ) O(n \log^2 n) O ( n log 2 n )
Sedgewick’s Sequence
H S e d g e w i c k = { 9 × 4 k − 9 × 2 k + 1 ∣ k ≥ 0 } ∪ { 4 k − 3 × 2 k + 1 ∣ k ≥ 2 } \mathcal{H}_{Sedgewick} = \{9 \times 4 ^k - 9 \times 2^k + 1 \,\, | \,\, k \ge 0\} \cup \{4^k - 3 \times 2^k + 1 \,\, | \,\, k \ge 2\} H S e d g e w i c k = { 9 × 4 k − 9 × 2 k + 1 ∣ k ≥ 0 } ∪ { 4 k − 3 × 2 k + 1 ∣ k ≥ 2 } 最坏复杂度 O ( n 4 / 3 ) O(n^{4 / 3}) O ( n 4 / 3 ) O ( n 7 / 6 ) O(n^{7 / 6}) O ( n 7 / 6 )